Главная » Социальная » Проекции точки и прямой, принадлежащих плоскости общего положения. Начертательная геометрия

Проекции точки и прямой, принадлежащих плоскости общего положения. Начертательная геометрия

Точка принадлежит плоскости, если она принадлежит какой-нибудь прямой, лежащей в этой плоскости.

Построение точки в плоскости сводится к двум операциям: построению в плоскости вспомогательной прямой и построению точки на этой прямой.

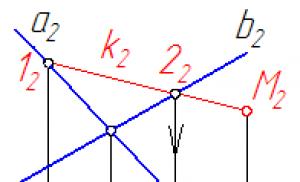
Задача: Плоскость S задана пересекающимися прямыми а и b (рис. 2-3). Точка М(М 2) принадлежит плоскости.

Найти М 1.

Краткая запись условия задачи: S(а Ç b), М(М 2) Î S; М 1 = ?

Решение: Через точку М 2 (рис. 2-4) проводим вспомогательную прямую

k Ì S: k 2 Ç a 2 =1 2 ; k 2 Ç b 2 =2 2 ;

затем находим горизонтальные проекции точек 1 и 2 по условию принадлежности прямым а и b соответственно; через две точки 1 1 и 2 1 проводим прямую k 1 и на ней, с помощью линии связи, находим точку М 1 . И таких прямых можно провести сколько угодно, то есть, вариантов решения бесчисленное множество.

Прямая принадлежит плоскости, если она:

1. Проходит через две точки плоскости;

2. Проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей в этой плоскости.

В предыдущем примере мы рассмотрели, как построить прямую в плоскости по двум точкам. Для второго случая плоскость Г зададим треугольником АВС.

Задача: Плоскость Г задана DАВС (рис. 2-5).

Точка М(М 1) принадлежит Г . Найти М 2 .

М(М 1) Î Г(АВС). М 2 = ?

Решение:

Через точку М 1 (рис.2-6) проведём прямую k , параллельную стороне треугольника АВ . Она пересечёт сторону АС в точке 1 : k 1 || A 1 B 1 ; k 1 A 1 Ç C 1 =1 1 ; с помощью линии связи найдём 1 2 , проведём k 2 параллельно А 2 В 2 ней найдём точку М 2 :

Алгоритмическая запись решения:

1 1 Î A 1 C 1 Þ 1 2 Î A 2 C 2 ; 1 2 Î k 2 , k 2 || A 2 B 2 ; M 2 Î k 2 .

Как вы думаете?

Сколько решений имеет эта задача?

Тео р ема 1: Прямая принадлежит плоскости, если она проходит через две точки, принадлежащие этой плоскости (рис. 43).

Тео р ема 2 : Точка принадлежит плоскости, если она расположена на прямой, лежащей в данной плоскости (рис. 44).

Конец работы -

Эта тема принадлежит разделу:

Основные методы проецирования. Сущность операции проецирования

Министерство образования и науки Российской Федерации казанский государственный университет..

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ:

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Казань 2010
Рекомендовано к печати Редакционно-издательским советом КГАСУ

Принятые обозначения и символика
1. Точки - прописными буквами латинского алфавита: А, В, С, D… или цифрами 1, 2, 3, 4… 2. Прямые и кривые линии– строчными буквами латинского алфавита: a, b, c,d…. 3. Поверхности

Центральное проецирование
В методе центрального проецирования все проецирующие лучи проходят через общую точку S. На рис.2 представлена кривая ℓ точками А, В, С и ее центральная проекци

Общие свойства проецирования
1. Проекцией точки является точка. 2. Проекцией прямой линии – прямая (частный случай: проекция прямой – точка, если прямая проходит через центр проекций).

Ортогональные проекции (прямоугольные проекции или метод Монжа)
Проецирование на одну плоскость проекций дает изображение, которое не позволяет однозначно определить форму и размеры изображенного предмета. Проекция точки А (рис.

Построение дополнительной профильной плоскости проекций
Выше было показано, что две проекции точки определяют ее положение в пространстве. Однако в практике изображения строительных конструкций, машин и различных инженерн

Октанты
Плоскости проекций при взаимном пересечении делят пространство на 8 трехгранных углов, или октантов (от лат. Octans – восьмая часть). Расчет их веде

Изображение линии на эпюре монжа
Простейшим геометрическим образом является линия. В начертательной геометрии приняты два способа образования линии: 1. Кинематический - линия рассматриваетс

Определитель линии
Определитель – это совокупность условий, задающих геометрический образ. Определитель линии – это точка и направлен

Прямые частного положения
Прямые частного положения – это прямые, параллельные или перпендикулярные какой-либо плоскости проекций. Существуют 6 прямых частного положения,

Принадлежность точки линии
Тео р ема: Точка принадлежит линии, если одноименные проекции точки лежат на одноименных проекциях линии (рис. 21). &nbs

Следом прямой
Горизонтальный след М – точка пересечения прямой с горизонтальной плоскостью проекций П1. Фронтальный след N – точка пересечения прямой с

Взаимное расположение прямых линий
Две прямые в пространстве могут: быть параллельными, пересекаться, скрещиваться. 1. Параллельными называются две прямые, которые лежат

Определение видимости геометрических элементов
При изображении непрозрачных предметов, в целях придания чертежу большей наглядности, проекции видимых элементов принято вычерчивать сплошными линиями, а невидимых –

Теорема о прямом угле
Тео р ема: Если одна сторона прямого угла параллельна какой-либо плоскости проекций, а другая сторона не перпендикулярна ей, то на эт

Определители плоскости
Раздел 3 Плоскость - простейшая поверхность I порядка, задается определителем: ∑ (Г, А), где: ∑ - обозначение п

Следы плоскости
Следами плоскости называются линии пересечения

Плоскость общего положения
Плоскость общего положения – это плоскость не параллельная и не перпендикулярная ни одной из плоскостей проекций (рис. 35). Все чертежи

Плоскости частного положения
Кроме рассмотренного общего случая плоскость, по отношению к плоскостям проекций, может занимать следующие частные положения: 1.

Главные линии плоскости
Из всех прямых, которые могут быть проведены в плоскости, следует выделить главные линии, к которым относятся: 1 Горизонталь плоскости

Преобразование чертежа
Раздел 4 В начертательной геометрии задачи решаются графически. Количество и характер геометрических построений, при этом,

Способ замены плоскостей проекций
Сущность способа замены плоскостей проекций заключается в том, что при неизменном положении заданного геометрического объекта в пространстве про

Проекций
Решение всех задач методом замены плоскостей проекций сводится к решению 4-х основных задач: 1. Замена плоскости проекций так, чтобы прямая общего положения стала прямой ур

Определение истинной длины отрезка прямой методом прямоугольного треугольника
Как известно, проекция прямой общего положения имеет искаженную величину. Для определения натуральной величины прямой, помимо вышеизложенного метода, используется

Способ вращения вокруг проецирующих осей
При решении задач на преобразование чертежа способом вращения положение заданных геометрических элементов изменяют путем вращения их вокруг проецирующей оси.

Вращение вокруг линии уровня
Данный способ применяется для преобразования плоскости общего положения в плоскость уровня и для определения натуральной величины плоской фигуры. Задача реш

Определитель поверхности
Раздел 5 Поверхности рассматриваются как непрерывное движение линии в пространстве по определенному закону, при этом линия, которая дв

Линейчатые поверхности
Линейчатые поверхности образуются непрерывным движением прямой образующей по некоторой направляющей, которая может быть прямой, ломаной или крив

Винтовые поверхности
Винтовые поверхности образуются винтовым движением прямой образующей. Это совокупность двух движений образующей: поступательного перемещения вдо

Поверхности вращения (ротационные) Определитель поверхностей вращения
Поверхности вращения получили широкое применение в архитектуре и строительстве. Они наиболее ярко выражают центричность архитектурной композиции и, кроме того, отлич

Поверхности, образованные вращением плоской кривой
Поверхности данной группы называются поверхностями общего положения. Алгоритм построения поверхностей (рис. 70): 1.

Поверхности, образованные вращением прямой
Определитель поверхности: Σ (i, ℓ), где i - ось вращения, ℓ - прямая.

Окружности
Определитель поверхности: Σ (i, ℓ), где i - ось вращения, ℓ - окружность. а) сфера (шар)

Пересечение поверхности геометрического тела с плоскостью
Построение линии пересечения поверхности с плоскостью применяется при образовании форм различных деталей строительных конструкций, при вычерчивании разрезов и планов

Взаимное пересечение поверхностей геометрических тел
Архитектурные сооружения и здания, различные фрагменты и детали являются сочетанием геометрических форм – призм, параллелепипедов, поверхностей вращения и более слож

Частные случаи пересечения поверхностей
Существуют два случая частного пересечения поверхностей: 1. Обе пересекающиеся поверхности – проецирующие.

Общий случай пересечения поверхностей
В этом случае обе пересекающиеся поверхности занимают общее положение в пространстве относительно плоскостей проекций. Задачи решаются с помощью посредников, в качес

Построение линии пересечения поверхностей второго порядка способом концентрических сфер
При пересечении поверхностей второго порядка линией пересечения в общем случае является пространственная кривая четвертого порядка, которая может распадаться на две

Теорема Монжа
Тео р ема: Если две поверхности вращения (второго порядка) описаны вокруг третьей или вписаны в нее, то линия пересечения их распадае

Пересечение прямой с поверхностью или плоскостью
Задачи на определение точек пересечения прямой с поверхностью (плоскостью) являются основными позиционными задачами начертательной геометрии, а также при построении

Развертки поверхностей
Раздел 7 Построение разверток – это инженерная задача, встречающаяся при выполнении технических деталей из тонкого листового материала, например, кожух вен

Развертка пирамиды
Задача. Построить развертку пирамиды SАВС. Определить на развертке положение точки М (рис. 98). Решение: Итак, для построения развертки поверхности, не

Развертка призмы
Рис.98 При построении развертки боковой поверхности призмы используют 2 способа: 1. способ нормального сечения; 2.

Развертки кривых поверхностей
В общем случае развертки кривых поверхностей выполняются способом триангуляции,т.е. заменой кривой поверхности на вписанную в нее гранную пов

Развертка прямого кругового конуса
Задача. Построить развертку прямого кругового конуса (рис. 101). Решение: Для построения развертки, в поверхность конуса вписывается n-гранная п

Развертка наклонного (эллиптического) конуса
Задача. Построить развертку наклонного конуса. Нанести на развертку линию пересечения конуса фронтально проецирующей плоскостью ∑ (рис. 102). Решение:

Развертка прямого кругового цилиндра
Задача. Построить развертку прямого кругового цилиндра (рис.103). Решение: Как и в рассмотренной выше задаче, в поверхность цилиндра вписывается n

Развертка поверхностей сферы и тора
Поверхность сферы и тора развертываются приближенно. Суть построения состоит в том, что развертку поверхности строят, разделив ее на равные доли (рис. 104) по меридианам, и каждую

Сущность метода проекций с числовыми отметками
Способы изображения, рассмотренные ранее, оказываются неприемлемыми при проектировании таких инженерных сооружений, как полотно железной или шоссейной дорог, дамбы, аэродромы, различного р

Изображение прямой
Прямая линия может быть задана проекциями двух любых ее точек. Итак, в пространстве расположена точка А, высота ее 3 единицы (рис. 107).

Заложение, превышение, интервал и уклон прямой
На рис. 109 изображена прямая АВ и ее проекция А1В3на нулевую пл

Градуирование прямой
Градуирование прямой– нахождение на проекции прямой точек, имеющих целые числовые отметки. Градуирование основано на способе пропорцион

Взаимное расположение прямых
Положение двух прямых в пространстве может быть определено по их проекциям на плоскость нулевого уровня (П0), если соблюдаются следующие условия: 1. Д

Изображение плоскости
Плоскость в проекциях с числовыми отметками изображается и задается теми же определителями, что и в ортогональных проекциях, а именно:

Взаимное расположение плоскостей
Две плоскости в пространстве могут либо быть параллельными между собой, либо пересекаться под прямым или острым-тупым углами. 1.

Пересекающиеся плоскости
(рис.123): Плоскости, масштабы уклонов которых не удовлетворяют хотя бы одному из указанных выше условий, пересекаются. Рис. 122

Пересечение прямой с плоскостью
Задача. Построить точку пересечения прямой А4В7с плоскостью, заданной масштабом уклонов ∑i. Решение:

Изображение поверхностей
В рассматриваемом методе все поверхности независимо от способа их образования изображают проекциями их горизонталей с указанием отметок, фикс

Поверхность одинакового ската (равного уклона)
Поверхностью одинакового ската называется линейчатая поверхность, все прямолинейные образующие которой составляют с некоторой плоскостью одинако

Топографическая поверхность
Существует большой класс поверхностей, строение которых не подчинено строгому математическому описанию. Такие поверхности называют топографическими.

Построение линии наибольшего ската топографической поверхности
Линии ската и одинакового уклона имеют широкое применение в инженерной практике. Знать направление линии ската нужно, в частности, для того, чтобы принять необходимы

Определение границ земляных работ
При проектировании железнодорожных трасс, шоссейных дорог, при возведении строительных площадок, необходимо определять объемы земляных работ, проводимых при сооружен

Заключение
Данное учебное пособие, как уже отмечалось, может быть использовано студентами специальностей 270106 «Производство строительных материалов, изделии и конструкций», 2

Ортогональные проекции (прямоугольные
проекции или метод Монжа)…………………………......... 9 1.5. Частные случаи расположения точек в пространстве………………………………………………11 1.6. Построение дополнительной профильной

Пересечение поверхности геометрического тела
с плоскостью………………………………………………47 6.2. Взаимное пересечение поверхностей геометрических тел……………………………………….52 6.3. Свойство проецирующей поверхности………………..52 6.4

Начертательная геометрия (краткий курс)
Учебное пособие Редакционно-издательский отдел Подписано в п

Задача: Плоскость S задана пересекающимися прямыми а и b (рис. 2-3). Точка М(М 2) принадлежит плоскости.

Найти М 1.

Краткая запись условия задачи: S(а Ç b), М(М 2)Î S; М 1 = ?

Решение: Через точку М 2 (рис. 2-4) проводим вспомогательную прямую

kÌ S: k 2 Ç a 2 =1 2 ; k 2 Ç b 2 =2 2 ;

Прямая принадлежит плоскости, если она:

1. Проходит через две точки плоскости;

Проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей в этой плоскости.

Задача: Плоскость Г задана DАВС (рис. 2-5).

Точка М(М 1) принадлежит Г . Найти М 2 .

М(М 1)Î Г(АВС). М 2 = ?

Решение:

Через точку М 1 (рис.2-6) проведём прямую k , параллельную стороне треугольника АВ . Она пересечёт сторону АС в точке 1 : k 1 || A 1 B 1 ; k 1 A 1 Ç C 1 =1 1 ; с помощью линии связи найдём 1 2 , проведём k 2 параллельно А 2 В 2 ней найдём точку М 2 :

Алгоритмическая запись решения:

1 1 Î A 1 C 1 Þ 1 2 Î A 2 C 2 ; 1 2 Î k 2 , k 2 || A 2 B 2 ; M 2 Î k 2 .

Как вы думаете?

Сколько решений имеет эта задача?

Плоскости частного положения

Плоскости, параллельные или перпендикулярные одной из плоскостей проекций, называются плоскостями частного положения.

Имеется две группы таких плоскостей:

Проецирующие плоскости
Плоскости уровня

Проецирующие плоскости

Если плоскость перпендикулярна только одной плоскости проекций, то она называется проецирующей.

Одна из её проекций вырождается в прямую линию, называемую главной проекцией и обладающую собирательными свойствами.

Горизонтально проецирующая плоскость

Это плоскость, перпендикулярная горизонтальной плоскости проекций: Г^^ П 1

(рис. 2-7а, 2-7б).

Графический признак:

Горизонтальная проекция Г 1 горизонтально проецирующей плоскости прямая линия, не параллельная и не перпендикулярная линиям связи. Это главная проекция.

Например:

Г ^^ П 1 - горизонтально проецирующая плоскость.

Г^ П 1 Þ Г 1 - прямая линия, главная проекция.

Ðb - угол наклона плоскости Г к П 2 .

Пространственный чертеж

3. Плоскость

3.1. Способы задания плоскости на ортогональных чертежах

Положение плоскости в пространстве определяется:

тремя точками, не лежащими на одной прямой;
прямой и точкой, взятой вне прямой;
двумя пересекающимися прямыми;
двумя параллельными прямыми;
плоской фигурой.

В соответствии с этим на эпюре плоскость может быть задана:

проекциями трёх точек, не лежащих на одной прямой (Рисунок 3.1,а);
проекциями точки и прямой (Рисунок 3.1,б);
проекциями двух пересекающихся прямых (Рисунок 3.1,в);
проекциями двух параллельных прямых (Рисунок 3.1,г);
плоской фигурой (Рисунок 3.1,д);
следами плоскости;
линией наибольшего ската плоскости.

Рисунок 3.1 - Способы задания плоскостей

Плоскость общего положения - это плоскость, которая не параллельна и не перпендикулярна ни одной из плоскостей проекций.
Следом плоскости называется прямая, полученная в результате пересечения заданной плоскости с одной из плоскостей проекций.

Плоскость общего положения может иметь три следа: горизонтальный απ1 , фронтальный απ2 и профильный απ3 , которые она образует при пересечении с известными плоскостями проекций: горизонтальной π1 , фронтальной π2 и профильной π3 (Рисунок 3.2).

Рисунок 3.2 - Следы плоскости общего положения

3.2. Плоскости частного положения

Плоскость частного положения - плоскость, перпендикулярная или параллельная плоскости проекций.

Плоскость, перпендикулярная плоскости проекций, называется проецирующей и на эту плоскость проекций она будет проецироваться в виде прямой линии.

Свойство проецирующей плоскости : все точки, линии, плоские фигуры, принадлежащие проецирующей плоскости, имеют проекции на наклонном следе плоскости (Рисунок 3.3).

Рисунок 3.3 - Фронтально-проецирующая плоскость,
которой принадлежат: точки A, B, C , линии AC, AB, BC ,
плоскость треугольника АВС

Горизонтально-проецирующая плоскость - плоскость, перпендикулярная горизонтальной плоскос ти проекций (Рисунок 3.4, б).

Фронтально-проецирующая плоскость - плоскость, перпендикулярная фронтальной плоскости проекций (Рисунок 3.4, а).

Профильно-проецирующая плоскость - плоскость, перпендикулярная профильной плоскости проекций.

Плоскости, параллельные плоскостям проекций, называются плоскостями уровня или дважды проецирующими плоскостями .

Горизонтальная плоскость уровня - плоскость, параллельная горизонтальной плоскости проекций (Рисунок 3.4, г).

Фронтальная плоскость уровня - плоскость, параллельная фронтальной плоскости проекций (Рисунок 3.4, в).

Профильная плоскость уровня - плоскость, параллельная профильной плоскости проекций (Рисунок 3.4, д).

Рисунок 3.4 - Эпюры плоскостей частного положения

3.3. Точка и прямая в плоскости

Точка принадлежит плоскости, если она принадлежит какой-либо прямой, лежащей в этой плоскости (Рисунок 3.5).

Рисунок 3.5. Принадлежность точки плоскости

α = m // n
D ∈ n ⇒ D ∈ α

Рисунок 3.6. Принадлежность прямой плоскости

α = m // n
D ∈ α
С ∈ α ⇒ СD ∈ α

Упражнение

Дана плоскость, заданная четырехугольником (Рисунок 3.7, а). Необходимо достроить горизонтальную проекцию вершины С .

а б
Рисунок 3.7 - Условие (а) и решение (б) задачи

Решение :

ABCD - плоский четырехугольник, задающий плоскость.
Проведём в нём диагонали AC и BD (Рисунок 3.7, б), которые являются пересекающимися прямыми, также задающими ту же плоскость.
Согласно признаку пересекающихся прямых, построим горизонтальную проекцию точки пересечения этих прямых K по её известной фронтальной проекции: A 2 C 2 ∩ B 2 D 2 =K 2 .
Восстановим линию проекционной связи до пересечения с горизонтальной проекцией прямой BD : на проекции диагонали B 1 D 1 строим К 1 .
Через А 1 К 1 проводим проекцию диагонали А 1 С 1 .
Точку С 1 получаем, посредством линии проекционной связи до пересечения её с горизонтальной проекцией продолженной диагонали А 1 К 1 .

3.4. Главные линии плоскости

В плоскости можно построить бесконечное множество прямых, но есть особые прямые, лежащие в плоскости, называемые главными линиями плоскости (Рисунок 3.8 - 3.11).

Прямой уровня или параллелью плоскости называется прямая, лежащая в данной плоскости и параллельная одной из плоскостей проекций.

Горизонталь или горизонтальная прямая уровня h (первая параллель ) - это прямая лежащая в данной плоскости и параллельная горизонтальной плоскости проекций (π1 ) (Рисунок 3.8, а; 3.9).

Рисунок 3.8.а. Горизонтальная прямая уровня в плоскости, заданной треугольником

Фронталь или фронтальная прямая уровня f (вторая параллель ) - это прямая лежащая в данной плоскости и параллельная фронтальной плоскости проекций (π2 ) (Рисунок 3.8, б; 3.10).

Рисунок 3.8.б. Фронтальная прямая уровня в плоскости, заданной треугольником

Профильная прямая уровня p (третья параллель ) - это прямая лежащая в данной плоскости и параллельная профильной плоскости проекций (π3 ) (Рисунок 3.8, в; 3.11).

Рисунок 3.8 в - Профильная прямая уровня в плоскости, заданной треугольником

Рисунок 3.9 - Горизонтальная прямая уровня в плоскости, заданной следами

Рисунок 3.10 - Фронтальная прямая уровня в плоскости, заданной следами

Рисунок 3.11 - Профильная прямая уровня в плоскости, заданной следами

3.5. Взаимное положение прямой и плоскости

Прямая по отношению к заданной плоскости может быть параллельной и может с ней иметь общую точку, то есть пересекаться.

3.5.1. Параллельность прямой плоскости

Признак параллельности прямой плоскости : прямая параллельна плоскости, если она параллельна любой прямой, принадлежащей этой плоскости (Рисунок 3.19).

Рисунок 3.19. Параллельность прямой плоскости

3.5.2. Пересечение прямой с плоскостью

Для построения линии пересечения прямой с плоскостью необходимо (Рисунок 3.20):

Заключить прямую а во вспомогательную плоскость β (в качестве вспомогательной плоскости следует выбирать плоскости частного положения);
Найти линию пересечения вспомогательной плоскости β с заданной плоскостью α;
Найти точку пересечения заданной прямой a с линией пересечения плоскостей MN .

Рисунок 3.20. Построение точки встречи прямой с плоскостью

Упражнение

Заданы: прямая АВ общего положения, плоскость σ ⊥ π1 (Рисунок 3.21). Построить точку пересечения прямой АВ с плоскостью σ.

Решение :

Плоскость σ - горизонтально-проецирующая, следовательно, горизонтальным следом σπ 1 (или σ 1 ) является прямая;
Точка К должна принадлежать прямой АВ ⇒ К 1 ∈ А 1 В 1 и заданной плоскости σ ⇒ К 1 ∈ σ 1 , следовательно, К 1 находится в точке пересечения проекций A 1 B 1 и σ 1 ;
Фронтальную проекцию точки К находим посредством линии проекционной связи: K 2 ∈ A 2 B 2 .

Рисунок 3.21. Пересечение прямой общего положения с плоскостью частного положения

Упражнение

Заданы: плоскость σ = ΔАВС - общего положения, прямая EF (Рисунок 3.22).
Требуется построить точку пересечения прямой EF с плоскостью σ.

А б
Рисунок 3.22. Пересечение прямой с плоскостью (а - модель, б - чертеж)

Решение :

Заключим прямую EF во вспомогательную плоскость, в качестве которой воспользуемся горизонтально-проецирующей плоскостью α (Рисунок 3.22, а);
Если α ⊥ π 1 , то на плоскость проекций π 1 плоскость α проецируется в прямую (горизонтальный след плоскости απ 1 или α 1 ), совпадающую с E 1 F 1 ;
Найдём прямую пересечения (1-2) проецирующей плоскости α с плоскостью σ (решение подобной задачи было рассмотрено ранее);
Прямая (1-2) и заданная прямая EF лежат в одной плоскости α и пересекаются в точке K .

Алгоритм решения задачи (Рисунок 3.22, б):

3.6. Определение видимости методом конкурирующих точек

Рисунок 3.23. Метод конкурирующих точек

При оценке положения данной прямой, необходимо определить - точка какого участка прямой расположена ближе (дальше) к нам, как к наблюдателям, при взгляде на плоскость проекций π1 или π2 .

Точки, которые в пространстве принадлежат разным объектам, а на одной из плоскостей проекций их проекции совпадают (то есть, две точки проецируются в одну), называются конкурирующими на этой плоскости проекций .

Необходимо отдельно определить видимость на каждой плоскости проекций!

Видимость на π2

Выберем точки, конкурирующие на π2 - точки 3 и 4 (рисунок 3.23). Пусть точка 3 ∈ ВС ∈ σ, точка 4 ∈ EF .

Чтобы определить видимость точек на плоскости проекций π2 надо определить расположение этих точек на горизонтальной плоскости проекций при взгляде на π2 .

Направление взгляда на π2 показано стрелкой.

По горизонтальным проекциям точек 3 и 4, при взгляде на π2 , видно, что точка 41 располагается ближе к наблюдателю, чем 31 .

41 ∈ E 1 F 1 → 4 ∈ EF ⇒ на π2 будет видима точка 4, лежащая на прямой EF , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена перед плоскостью σ и будет видима до точки K

Видимость на π1

Для определения видимости выберем точки, конкурирующие на π1 - точки 2 и 5.

Чтобы определить видимость точек на плоскости проекций π1 надо определить расположение этих точек на фронтальной плоскости проекций при взгляде на π1 .

Направление взгляда на π1 показано стрелкой.

По фронтальным проекциям точек 2 и 5, при взгляде на π1 , точка 22 располагается ближе к наблюдателю, чем 52 .

22 ∈ А 2 В 2 → 2 ∈ АВ ⇒ на π1 будет видима точка 2, лежащая на прямой АВ , следовательно, прямая EF на участке рассматриваемых конкурирующих точек расположена под плоскостью σ и будет невидима до точки K - пересечения прямой с плоскостью σ.

Видимой из двух конкурирующих точек будет та, у которой координата «Z » или(и) «Y » больше.

3.7. Перпендикулярность прямой плоскости

Признак перпендикулярности прямой плоскости : прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым, лежащим в данной плоскости.

Рисунок 3.24. Задание прямой, перпендикулярной плоскости

Если прямая перпендикулярна плоскости, то на эпюре: проекции прямой перпендикулярны наклонным проекциям горизонтали и фронтали, лежащих в плоскости, или следам плоскости (Рисунок 3.24).

Пусть прямая p перпендикулярна плоскости σ = Δ АВС и проходит через точку K .
Построим горизонталь и фронталь в плоскости σ = Δ АВС :
A -1 ∈ σ; A -1 // π 1 ; С -2 ∈ σ; С -2 // π 2 .
Восстановим из точки K перпендикуляр к заданной плоскости:
p 1 ⊥ h 1 и p 2 ⊥ f 2 .

3.8. Взаимное положение двух плоскостей

Две плоскости могут быть параллельными и пересекающимися между собой.

3.8.1. Параллельность плоскостей

Признак параллельности двух плоскостей : две плоскости взаимно параллельны, если две пересекающиеся прямые одной плоскости соответственно параллельны двум пересекающимся прямым другой плоскости.

Упражнение

Задана плоскость общего положения α = ΔАВС и точка F ∉ α (Рисунок 3.12).
Через точку F провести плоскость σ, параллельную плоскости α.

Рисунок 3.12. Построение плоскости, параллельной заданной

Решение :

Через точку F проводим прямую m , параллельную, например, АВ .
Через точку F , или же через любую точку, принадлежащую m , проводим прямую n , параллельную, например, ВС , причём m ∩ n .
σ = m ∩n и σ // α по определению.

3.8.2. Пересечение плоскостей

Результатом пересечения 2-х плоскостей является прямая. Любая прямая однозначно на плоскости или в пространстве может быть задана двумя точками. Поэтому для того, чтобы построить линию пересечения двух плоскостей, следует найти две точки, общие для обеих плоскостей, после чего соединить их.

Рассмотрим примеры пересечения двух плоскостей при различных способах их задания: следами; тремя точками, не лежащими на одной прямой; параллельными прямыми; пересекающимися прямыми и др.

Упражнение

Две плоскости α и β заданы следами (Рисунок 3.13). Построить линию пересечения плоскостей.

Рисунок 3.13. Пересечение плоскостей, заданных следами

Порядок построения линии пересечения плоскостей :

Найти точку пересечения горизонтальных следов - это точка М (её проекции М 1 и М 2 , при этом М 1 = М , т.к. М - точка частного положения, принадлежащая плоскости π 1 ).
Найти точку пересечения фронтальных следов - это точка N (её проекции N 1 и N 2 , при этом N 2 = N , т.к. N - точка частного положения, принадлежащая плоскости π 2 ).
Построить линию пересечения плоскостей, соединив одноименные проекции полученных точек: М 1 N 1 и М 2 N 2 .

МN - линия пересечения плоскостей.

Упражнение

Задана плоскость α = ΔАВС , плоскость σ - горизонтально-проецирующая (σ ⊥ π1 ) ⇒ σ1 - горизонтальный след плоскости (Рисунок 3.14).
Построить линию пересечения этих плоскостей.

Решение :

Так как плоскость σ пересекает стороны АВ и АС треугольника АВС , то точки пересечения K и L этих сторон с плоскостью σ являются общими для обеих заданных плоскостей, что позволит, соединив их, найти искомую линию пересечения.

Точки могут быть найдены как точки пересечения прямых с проецирующей плоскостью: находим горизонтальные проекции точек K и L , то есть K 1 и L 1 на пересечении горизонтального следа (σ1 ) заданной плоскости σ с горизонтальными проекциями сторон ΔАВС : А 1 В 1 и A 1 C 1 . После чего посредством линий проекционной связи находим фронтальные проекции этих точек K 2 и L 2 на фронтальных проекциях прямых АВ и АС . Соединим одноимённые проекции: K 1 и L 1 ; K2 и L 2 . Линия пересечения заданных плоскостей построена.

Алгоритм решения задачи :

АВ ∩ σ = K ⇒ А 1 В 1 ∩ σ1 = K 1 → K 2
АС ∩ σ = L ⇒ A 1 C 1 ∩ σ1 = L 1 → L 2
KL - линия пересечения ΔАВС и σ (α ∩ σ = KL ).

Рисунок 3.14. Пересечение плоскостей общего и частного положения

Упражнение

Заданы плоскости α = m // n и плоскость β = ΔАВС (Рисунок 3.15).
Построить линию пересечения заданных плоскостей.

Решение :

Чтобы найти точки, общие для обеих заданных плоскостей и задающие линию пересечения плоскостей α и β, необходимо воспользоваться вспомогательными плоскостями частного положения.
В качестве таких плоскостей выберем две вспомогательные плоскости частного положения, например: σ // τ ; σ ⊥ π 2 ; τ ; ⊥ π 2 .
Вновь введённые плоскости пересекаются с каждой из заданных плоскостей α и β по прямым, параллельным друг другу, так как σ // τ ;:
- результатом пересечения плоскостей α, σ и τ ; являются прямые (4-5) и (6-7);
- результатом пересечения плоскостей β, σ и τ ; являются прямые (3-2) и (1-8).
Прямые (4-5) и (3-2) лежат в плоскости σ; точка их пересечения М одновременно лежит в плоскостях α и β, то есть на прямой пересечения этих плоскостей;
Решение :
1. Воспользуемся вспомогательными секущими плоскостями частного положения. Введём их так, чтобы сократить количество построений. Например, введём плоскость σ ⊥ π2 , заключив прямую а во вспомогательную плоскость σ (σ ∈ a ).
2. Плоскость σ пересекает плоскость α по прямой (1-2), а σ ∩ β = а . Следовательно (1-2) ∩ а = K .
3. Точка К принадлежит обеим плоскостям α и β.
4. Следовательно, точка K , является одной из искомых точек, через которые проходит прямая пересечения заданных плоскостей α и β.
5. Для нахождения второй точки, принадлежащей прямой пересечения α и β, заключим прямую b во вспомогательную плоскость τ ⊥π2 (τ ∈ b ).
6. Соединив точки K и L , получим прямую пересечения плоскостей α и β.
3.8.3. Взаимно перпендикулярные плоскости
Плоскости взаимно перпендикулярны, если одна из них проходит через перпендикуляр к другой.

Упражнение
Задана плоскость σ ⊥ π2 и прямая общего положения - DE (Рисунок 3.17).
Требуется построить через DE плоскость τ ⊥ σ.

Решение :
Проведем перпендикуляр CD к плоскости σ - C 2 D 2 ⊥ σ2 .

Рисунок 3.17 - Построение плоскости, перпендикулярной к заданной плоскости

По теореме о проецировании прямого угла C 1 D 1 должна быть параллельна оси проекций. Пересекающиеся прямые CD ∩ DE задают плоскость τ . Итак, τ ⊥ σ.
Аналогичные рассуждения, в случае плоскости общего положения.

Упражнение
Задана плоскость α = ΔАВС и точка K вне плоскости α.
Требуется построить плоскость β ⊥ α, проходящую через точку K .

Алгоритм решения (Рисунок 3.18):
1. Построим горизонталь h и фронталь f в заданной плоскости α = Δ АВС ;
2. Через точку K проведём перпендикуляр b к плоскости α (по теореме о перпендикуляре к плоскости: если прямая перпендикулярна плоскости, то её проекции перпендикулярны к наклонным проекциям горизонтали и фронтали, лежащих в плоскости: b 2 ⊥ f 2 ; b 1 ⊥ h 1 );
3. Задаем плоскость β любым способом, учитывая, например, β = a ∩ b , таким образом, плоскость, перпендикулярная к заданной, построена: α ⊥ β.
Рисунок 3.18 - Построение плоскости, перпендикулярной к заданной ΔАВС
Задачи для самостоятельной работы

1. Задана плоскость α = m // n . Известно, что K ∈ α.
Постройте фронтальную проекцию точки К .

Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.

Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.

Принадлежность прямой плоскости определяется по одному из двух признаков:

а) прямая проходит через две точки, лежащие в этой плоскости;

б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.

Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС . Требуется построить недостающую проекцию D 1 точки D , принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).

Через точку D 2 проводим проекцию прямой d , лежащей в плоскости DАВС , пересекающую одну из сторон треугольника и точку А 2 . Тогда точка 1 2 принадлежит прямым А 2 D 2 и C 2 В 2 . Следовательно, можно получить ее горизонтальную проекцию 1 1 на C 1 В 1 по линии связи. Соединив точки 1 1 и А 1 , получаем горизонтальную проекцию d 1 . Ясно, что точка D 1 принадлежит ей и лежит на линии проекционной связи с точкой D 2 .

Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.

Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.

Для того, чтобы определить принадлежит ли точка Е плоскости DАВС , проведем через ее фронтальную проекцию Е 2 прямую а 2 . Считая, что прямая а принадлежит плоскости DАВС , построим ее горизонтальную проекцию а 1 по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а 1 не проходит через точку Е 1 . Следовательно, точка Е ÏDАВС .

В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в 2 построить другую в 1 * считая, что вÌDАВС . Как видим, в 1 * и в 1 не совпадают. Следовательно, прямая в Ë DАВС .

Линии уровня в плоскости

Определение линий уровня было дано ранее. Линии уровня, принадлежащие данной плоскости, называются главными . Эти линии (прямые) играют существенную роль при решении ряда задач начертательной геометрии.

Рассмотрим построение линий уровня в плоскости, заданной треугольником (рис. 2.7).

Рис. 2.7. Построение главных линий плоскости, заданной треугольником

Горизонталь плоскости DАВС начинаем с вычерчивания ее фронтальной проекции h 2 , которая, как известно, параллельна оси ОХ . Поскольку эта горизонталь принадлежит данной плоскости, то она проходит через две точки плоскости DАВС , а именно, точки А и 1. Имея их фронтальные проекции А 2 и 1 2 , по линии связи получим горизонтальные проекции (А 1 уже есть) 1 1 . Соединив точки А 1 и 1 1 , имеем горизонтальную проекцию h 1 горизонтали плоскости DАВС . Профильная проекция h 3 горизонтали плоскости DАВС будет параллельна оси ОХ по определению.

Фронталь плоскости DАВС строится аналогично (рис. 2.7) с той лишь разницей, что ее вычерчивание начинается с горизонтальной проекции f 1 , так как известно, что она параллельна оси ОХ. Профильная проекция f 3 фронтали должна быть параллельна оси ОZ и пройти через проекции С 3 , 2 3 тех же точек С и 2.

Профильная линия плоскости DАВС имеет горизонтальную р 1 и фронтальную р 2 проекции, параллельные осям OY и OZ , а профильную проекцию р 3 можно получить по фронтальной, используя точки пересечения В и 3 с D АВС .