Главная » Новости » Как посчитать среднее квадратичное. Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации

Как посчитать среднее квадратичное. Дисперсия, среднеквадратичное (стандартное) отклонение, коэффициент вариации

$X$. Для начала напомним следующее определение:

Определение 1

Генеральная совокупность -- совокупность случайно отобранных объектов данного вида, над которыми проводят наблюдения с целью получения конкретных значений случайной величины, проводимых в неизменных условиях при изучении одной случайной величины данного вида.

Определение 2

Генеральная дисперсия -- среднее арифметическое квадратов отклонений значений вариант генеральной совокупности от их среднего значения.

Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда генеральная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае генеральная дисперсия вычисляется по формуле:

С этим понятием также связано понятие генерального среднего квадратического отклонения.

Определение 3

Генеральное среднее квадратическое отклонение

\[{\sigma }_г=\sqrt{D_г}\]

Выборочная дисперсия

Пусть нам дана выборочная совокупность относительно случайной величины $X$. Для начала напомним следующее определение:

Определение 4

Выборочная совокупность -- часть отобранных объектов из генеральной совокупности.

Определение 5

Выборочная дисперсия -- среднее арифметическое значений вариант выборочной совокупности.

Пусть значения вариант $x_1,\ x_2,\dots ,x_k$ имеют, соответственно, частоты $n_1,\ n_2,\dots ,n_k$. Тогда выборочная дисперсия вычисляется по формуле:

Рассмотрим частный случай. Пусть все варианты $x_1,\ x_2,\dots ,x_k$ различны. В этом случае $n_1,\ n_2,\dots ,n_k=1$. Получаем, что в этом случае выборочная дисперсия вычисляется по формуле:

С этим понятием также связано понятие выборочного среднего квадратического отклонения.

Определение 6

Выборочное среднее квадратическое отклонение -- квадратный корень из генеральной дисперсии:

\[{\sigma }_в=\sqrt{D_в}\]

Исправленная дисперсия

Для нахождения исправленной дисперсии $S^2$ необходимо умножить выборочную дисперсию на дробь $\frac{n}{n-1}$, то есть

С этим понятием также связано понятие исправленного среднего квадратического отклонения, которое находится по формуле:

В случае, когда значение вариант не являются дискретными, а представляют из себя интервалы, то в формулах для вычисления генеральной или выборочной дисперсий за значение $x_i$ принимается значение середины интервала, которому принадлежит $x_i.$

Пример задачи на нахождение дисперсии и среднего квадратического отклонения

Пример 1

Выборочная совокупность задана следующей таблицей распределения:

Рисунок 1.

Найдем для нее выборочную дисперсию, выборочное среднее квадратическое отклонение, исправленную дисперсию и исправленное среднее квадратическое отклонение.

Для решения этой задачи для начала сделаем расчетную таблицу:

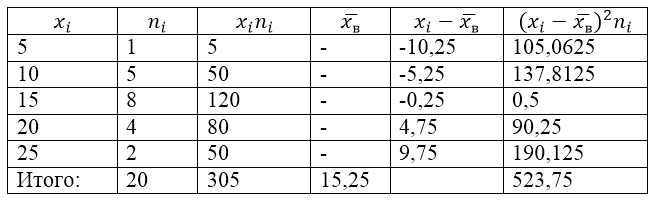
Рисунок 2.

Величина $\overline{x_в}$ (среднее выборочное) в таблице находится по формуле:

\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}\]

\[\overline{x_в}=\frac{\sum\limits^k_{i=1}{x_in_i}}{n}=\frac{305}{20}=15,25\]

Найдем выборочную дисперсию по формуле:

Выборочное среднее квадратическое отклонение:

\[{\sigma }_в=\sqrt{D_в}\approx 5,12\]

Исправленная дисперсия:

\[{S^2=\frac{n}{n-1}D}_в=\frac{20}{19}\cdot 26,1875\approx 27,57\]

Исправленное среднее квадратическое отклонение.

Среднее квадратическое отклонение

Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, ĸᴏᴛᴏᴩᴏᴇ называют стандартом (или стандартным отклонение).Среднее квадратическое отклонение () равно квадратному корню из среднего квадрата отклонений отдельных значений признака от средней арифметической:

Среднее квадратическое отклонение простое:

Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных:

Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: ~ 1,25.

Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности.

18.Дисперсия, ее виды, среднеквадратическое отклонение.

Диспе́рсия случа́йной величины́ - мера разброса данной случайной величины, т. е. её отклонения отматематического ожидания. В статистике часто употребляется обозначение или . Квадратный корень из дисперсии принято называтьсреднеквадрати́чным отклоне́нием , станда́ртным отклоне́нием или стандартным разбросом.

Общая дисперсия (σ 2 ) измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Вместе с тем, благодаря методу группировок можно выделить и измерить вариацию, обусловленную группировочным признаком, и вариацию, возникающую под влиянием неучтенных факторов.

Межгрупповая дисперсия (σ 2 м.гр ) характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака – фактора, положенного в основание группировки.

Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние , среднеквадрати́чное отклоне́ние , квадрати́чное отклоне́ние ; близкие термины:станда́ртное отклоне́ние , станда́ртный разбро́с ) - в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величиныотносительно её математического ожидания. При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическоесовокупности выборок.

Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического, при построении доверительных интервалов, при статистической проверке гипотез, при измерении линейной взаимосвязи между случайными величинами. Определяется какквадратный корень из дисперсии случайной величины.

Среднеквадратическое отклонение:

Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на базе несмещённой оценки её дисперсии):

где - дисперсия; - i -й элемент выборки; - объём выборки; - среднее арифметическое выборки:

Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. При этом оценка на базе оценки несмещённой дисперсии является состоятельной.

19.Сущность, область применения и порядок определения моды и медианы.

Кроме степенных средних в статистике для относительной характеристики величины варьирующего признака и внутреннего строения рядов распределения пользуются структурными средними, которые представлены,в основном, модой и медианой .

Мода - это наиболее часто встречающийся вариант ряда. Мода применяется, к примеру, при определении размера одежды, обуви, пользующейся наибольшим спросом у покупателей. Модой для дискретного ряда является варианта͵ обладающая наибольшей частотой. При вычислении моды для интервального вариационного ряда крайне важно сначала определить модальный интервал (по максимальной частоте), а затем - значение модальной величины признака по формуле:

§ - значение моды

§ - нижняя граница модального интервала

§ - величина интервала

§ - частота модального интервала

§ - частота интервала, предшествующего модальному

§ - частота интервала, следующего за модальным

Медиана - это значение признака, ĸᴏᴛᴏᴩᴏᴇ лежит в базе ранжированного ряда и делит данный ряд на две равные по численности части.

Для определения медианы в дискретном ряду при наличии частот сначала вычисляют полусумму частот , а затем определяют, какое значение варианта приходится на нее. (В случае если отсортированный ряд содержит нечетное число признаков, то номер медианы вычисляют по формуле:

М е = (n (число признаков в совокупности) + 1)/2,

в случае четного числа признаков медиана будет равна средней из двух признаков находящихся в середине ряда).

При вычислении медианы для интервального вариационного ряда сначала определяют медианный интервал, в пределах которого находится медиана, а затем - значение медианы по формуле:

§ - искомая медиана

§ - нижняя граница интервала, который содержит медиану

§ - величина интервала

§ - сумма частот или число членов ряда

§ - сумма накопленных частот интервалов, предшествующих медианному

§ - частота медианного интервала

Пример . Найти моду и медиану.

Решение : В данном примере модальный интервал находится в пределах возрастной группы 25-30 лет, так как на данный интервал приходится наибольшая частота (1054).

Рассчитаем величину моды:

Это значит что модальный возраст студентов равен 27 годам.

Вычислим медиану. Медианный интервал находится в возрастной группе 25-30 лет, так как в пределах этого интервала расположена варианта͵ которая делит совокупность на две равные части (Σf i /2 = 3462/2 = 1731). Далее подставляем в формулу необходимые числовые данные и получаем значение медианы:

Это значит что одна половина студентов имеет возраст до 27,4 года, а другая свыше 27,4 года.

Кроме моды и медианы бывают использованы такие показатели, как квартили, делящие ранжированный ряд на 4 равные части, децили -10 частей и перцентили - на 100 частей.

20.Понятие выборочного наблюдения и область его применения.

Выборочное наблюдение применяется, когда применение сплошного наблюдения физически невозможно из-за большого массива данных или экономически нецелесообразно . Физическая невозможность имеет место, к примеру, при изучении пассажиропотоков, рыночных цен, семейных бюджетов. Экономическая нецелесообразность имеет место при оценке качества товаров, связанной с их уничтожением, к примеру, дегустация, испытание кирпичей на прочность и т.п.

Статистические единицы, отобранные для наблюдения, составляют выборочную совокупность или выборку , а весь их массив - генеральную совокупность (ГС). При этом число единиц в выборке обозначают n , а во всей ГС - N . Отношение n/N принято называть относительный размер или доля выборки .

Качество результатов выборочного наблюдения зависит от репрезентативности выборки , то есть от того, насколько она представительна в ГС. Для обеспечения репрезентативности выборки крайне важно соблюдать принцип случайности отбора единиц , который предполагает, что на включение единицы ГС в выборку не может повлиять какой-либо иной фактор кроме случая.

Существует 4 способа случайного отбора в выборку:

Собственно случайный отбор или ʼʼметод лотоʼʼ, когда статистическим величинам присваиваются порядковые номера, заносимые на определенные предметы (к примеру, бочонки), которые затем перемешиваются в некоторой емкости (к примеру, в мешке) и выбираются наугад. На практике данный способ осуществляют с помощью генератора случайных чисел или математических таблиц случайных чисел.
Механический отбор, согласно которому отбирается каждая (N/n )-я величина генеральной совокупности. К примеру, в случае если она содержит 100 000 величин, а требуется выбрать 1 000, то в выборку попадет каждая 100 000 / 1000 = 100-я величина. Причем, в случае если они не ранжированы, то первая выбирается наугад из первой сотни, а номера других будут на сотню больше. К примеру, в случае если первой оказалась единица № 19, то следующей должна быть № 119, затем № 219, затем № 319 и т.д. В случае если единицы генеральной совокупности ранжированы, то первой выбирается № 50, затем № 150, затем № 250 и так далее.
Отбор величин из неоднородного массива данных ведется стратифицированным (расслоенным) способом, когда генеральная совокупность предварительно разбивается на однородные группы, к которым применяется случайный или механический отбор.
Особый способ составления выборки представляет собой серийный отбор, при котором случайно или механически выбирают не отдельные величины, а их серии (последовательности с какого-то номера по какой-то подряд), внутри которых ведут сплошное наблюдение.

Качество выборочных наблюдений зависит и от типа выборки : повторная или бесповторная. При повторном отборе попавшие в выборку статистические величины или их серии после использования возвращаются в генеральную совокупность, имея шанс попасть в новую выборку. При этом у всех величин генеральной совокупности одинаковая вероятность включения в выборку. Бесповторный отбор означает, что попавшие в выборку статистические величины или их серии после использования не возвращаются в генеральную совокупность, а потому для остальных величин последней повышается вероятность попадания в следующую выборку.

Бесповторный отбор дает более точные результаты, в связи с этим применяется чаще. Но есть ситуации, когда его применить нельзя (изучение пассажиропотоков, потребительского спроса и т.п.) и тогда ведется повторный отбор.

21.Предельная ошибка выборки наблюдения, средняя ошибка выборки, порядок их расчета.

Рассмотрим подробно перечисленные выше способы формирования выборочной совокупности и возникающие при этом ошибки репрезентативности. Собственно-случайная выборка основывается на отборе единиц из генеральной совокупности наугад без каких-либо элементов системности. Технически собственно-случайный отбор проводят методом жеребьевки (к примеру, розыгрыши лотерей) или по таблице случайных чисел.

Собственно-случайный отбор ʼʼв чистом видеʼʼ в практике выборочного наблюдения применяется редко, но он является исходным среди других видов отбора, в нем реализуются основные принципы выборочного наблюдения. Рассмотрим некоторые вопросы теории выборочного метода и формулы ошибок для простой случайной выборки.

Ошибка выборочного наблюдения - ϶ᴛᴏ разность между величиной параметра в генеральной совокупности, и его величиной, вычисленной по результатам выборочного наблюдения. Важно заметить, что для средней количественного признака ошибка выборки определяется

Показатель принято называть предельной ошибкой выборки. Выборочная средняя является случайной величиной, которая может принимать различные значения исходя из того, какие единицы попали в выборку. Следовательно, ошибки выборки также являются случайными величинами и могут принимать различные значения. По этой причине определяют среднюю из возможных ошибок – среднюю ошибку выборки , которая зависит от:

· объёма выборки: чем больше численность, тем меньше величина средней ошибки;

· степени изменения изучаемого признака: чем меньше вариация признака, а, следовательно, и дисперсия, тем меньше средняя ошибка выборки.

При случайном повторном отборе средняя ошибка рассчитывается . Практически генеральная дисперсия точно не известна, но в теории вероятности доказано, что . Так как величина при достаточно больших n близка к 1, можно считать, что . Тогда средняя ошибка выборки должна быть рассчитана: . Но в случаях малой выборки (при n<30) коэффициент крайне важно учитывать, и среднюю ошибку малой выборки рассчитывать по формуле .

При случайной бесповторной выборке приведенные формулы корректируются на величину . Тогда средняя ошибка бесповторной выборки: и . Т.к. всегда меньше , то множитель () всегда меньше 1. Это значит, что средняя ошибка при бесповторном отборе всегда меньше, чем при повторном. Механическая выборка применяется, когда генеральная совокупность каким-либо способом упорядочена (к примеру, списки избирателей по алфавиту, телефонные номера, номера домов, квартир). Отбор единиц осуществляется через определенный интервал, который равен обратному значению процента выборки. Так при 2% выборке отбирается каждая 50 единица =1/0,02 , при 5% каждая 1/0,05=20 единица генеральной совокупности.

Начало отсчета выбирается разными способами: случайным образом, из середины интервала, со сменой начала отсчета. Главное при этом – избежать систематической ошибки. К примеру, при 5% выборке, в случае если первой единицей выбрана 13-я, то следующие 33, 53, 73 и т.д.

По точности механический отбор близок к собственно-случайной выборке. По этой причине для определения средней ошибки механической выборки используют формулы собственно-случайного отбора.

При типическом отборе обследуемая совокупность предварительно разбивается на однородные, однотипные группы. К примеру, при обследовании предприятий это бывают отрасли, подотрасли, при изучении населения – районы, социальные или возрастные группы. Далее осуществляется независимый выбор из каждой группы механическим или собственно-случайным способом.

Типическая выборка дает более точные результаты по сравнению с другими способами. Типизация генеральной совокупности обеспечивает представительство в выборке каждой типологической группы, что позволяет исключить влияние межгрупповой дисперсии на среднюю ошибку выборки. Следовательно, при нахождении ошибки типической выборки согласно правилу сложения дисперсий () крайне важно учесть лишь среднюю из групповых дисперсий. Тогда средняя ошибка выборки: при повторном отборе , при бесповторном отборе , где – средняя из внутригрупповых дисперсий в выборке.

Серийный (или гнездовой) отбор применяется в случае, когда генеральная совокупность разбита на серии или группы до начала выборочного обследования. Этими сериями бывают упаковки готовой продукции, студенческие группы, бригады. Серии для обследования выбираются механическим или собственно-случайным способом, а внутри серии производится сплошное обследование единиц. По этой причине средняя ошибка выборки зависит только от межгрупповой (межсерийной) дисперсии, которая вычисляется по формуле: где r – число отобранных серий; – средняя і-той серии. Средняя ошибка серийной выборки рассчитывается: при повторном отборе , при бесповторном отборе , где R – общее число серий. Комбинированный отбор представляет собой сочетание рассмотренных способов отбора.

Средняя ошибка выборки при любом способе отбора зависит главным образом от абсолютной численности выборки и в меньшей степени – от процента выборки. Предположим, что проводится 225 наблюдений в первом случае из генеральной совокупности в 4500 единиц и во втором – в 225000 единиц. Дисперсии в обоих случаях равны 25. Тогда в первом случае при 5 %-ном отборе ошибка выборки составит: Во втором случае при 0,1 %-ном отборе она будет равна:

Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, при уменьшении процента выборки в 50 раз, ошибка выборки увеличилась незначительно, так как численность выборки не изменилась. Предположим, что численность выборки увеличили до 625 наблюдений. В этом случае ошибка выборки равна: Увеличение выборки в 2,8 раза при одной и той же численности генеральной совокупности снижает размеры ошибки выборки более чем в 1,6 раза.

22.Методы и способы формирования выборочной совокупности.

В статистике применяются различные способы формирования выборочных совокупностей, что обусловливается задачами исследования и зависит от специфики объекта изучения.

Основным условием проведения выборочного обследования является предупреждение возникновения систематических ошибок, возникающих вследствие нарушения принципа равных возможностей попадания в выборку каждой единицы генеральной совокупности. Предупреждение систематических ошибок достигается в результате применения научно обоснованных способов формирования выборочной совокупности.

Существуют следующие способы отбора единиц из генеральной совокупности: 1) индивидуальный отбор - в выборку отбираются отдельные единицы; 2) групповой отбор - в выборку попадают качественно однородные группы или серии изучаемых единиц; 3) комбинированный отбор - это комбинация индивидуального и группового отбора. Способы отбора определяются правилами формирования выборочной совокупности.

Выборка должна быть:

собственно-случайная состоит в том, что выборочная совокупность образуется в результате случайного (непреднамеренного) отбора отдельных единиц из генеральной совокупности. При этом количество отобранных в выборочную совокупность единиц обычно определяется исходя из принятой доли выборки. Доля выборки есть отношение числа единиц выборочной совокупности n к численности единиц генеральной совокупности N, ᴛ.ᴇ.

механическая состоит в том, что отбор единиц в выборочную совокупность производится из генеральной совокупности, разбитой на равные интервалы (группы). При этом размер интервала в генеральной совокупности равен обратной величине доли выборки. Так, при 2%-ной выборке отбирается каждая 50-я единица (1:0,02), при 5%-ной выборке - каждая 20-я единица (1:0,05) и т.д. Τᴀᴋᴎᴍ ᴏϬᴩᴀᴈᴏᴍ, в соответствии с принятой долей отбора, генеральная совокупность как бы механически разбивается на равновеликие группы. Из каждой группы в выборку отбирается лишь одна единица.
типическая – при которойгенеральная совокупность вначале расчленяется на однородные типические группы. Далее из каждой типической группы собственно-случайной или механической выборкой производится индивидуальный отбор единиц в выборочную совокупность. Важной особенностью типической выборки является то, что она дает более точные результаты по сравнению с другими способами отбора единиц в выборочную совокупность;
серийная - при которой генеральную совокупность делят на одинаковые по объёму группы - серии. В выборочную совокупность отбираются серии. Внутри серий производится сплошное наблюдение единиц, попавших в серию;
комбинированная - выборка должна быть двухступенчатой. При этом генеральная совокупность сначала разбивается на группы. Далее производят отбор групп, а внутри последних осуществляется отбор отдельных единиц.

В статистике различают следующие способы отбора единиц в выборочную совокупность:

одноступенчатая выборка - каждая отобранная единица сразу же подвергается изучению по заданному признаку (собственно-случайная и серийная выборки);
многоступенчатая выборка - производят подбор из генеральной совокупности отдельных групп, а из групп выбираются отдельные единицы (типическая выборка с механическим способом отбора единиц в выборочную совокупность).

Кроме того различают :

повторный отбор – по схеме возвращенного шара. При этом каждая попавшая в выборку единица иди серия возвращается в генеральную совокупность и в связи с этим имеет шанс снова попасть в выборку;
бесповторный отбор – по схеме невозвращенного шара. Он имеет более точные результаты при одном и том же объёме выборки.

23.Определение крайне важно го объёма выборки (использование таблицы Стьюдента).

Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически крайне важно сть соблюдения этого принципа представлена в доказательствах предельных теорем теории вероятностей, которые позволяют установить, какой объём единиц следует выбрать из генеральной совокупности, чтобы он был достаточным и обеспечивал репрезентативность выборки.

Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки всегда связано с увеличением объёма выборки, в связи с этим уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объём выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Расчет крайне важно го объёма выборки строится с помощью формул, выведенных из формул предельных ошибок выборки (А), соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объёма выборки (n) имеем:

Суть этой формулы – в том, что при случайном повторном отборе крайне важно й численности объём выборки прямо пропорционален квадрату коэффициента доверия (t2) и дисперсии вариационного признака (?2) и обратно пропорционален квадрату предельной ошибки выборки (?2). В частности, с увеличением предельной ошибки в два раза необходимая численность выборки должна быть уменьшена в четыре раза. Из трех параметров два (t и?) задаются исследователем. При этом исследователь исходя из цели

и задач выборочного обследования должен решить вопрос: в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта? В одном случае его может больше устраивать надежность полученных результатов (t), нежели мера точности (?), в другом – наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает, в связи с этим в практике принято задавать величину предельной ошибки выборки, как правило, в пределах до 10 % предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по разному: использовать данные подобных ранее проведенных обследований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку.

Наиболее сложно установить при проектировании выборочного наблюдения третий параметр в формуле (5.2) – дисперсию выборочной совокупности. В этом случае крайне важно использовать всю информацию, имеющуюся в распоряжении исследователя, полученную в ранее проведенных подобных и пробных обследованиях.

Вопрос об определении крайне важно й численности выборки усложняется, в случае если выборочное обследование предполагает изучение нескольких признаков единиц отбора. В этом случае средние уровни каждого из признаков и их вариация, как правило, различны, и в связи с этим решить вопрос о том, дисперсии какого из признаков отдать предпочтение, возможно лишь с учетом цели и задач обследования.

При проектировании выборочного наблюдения предполагаются заранее заданная величина допустимой ошибки выборки в соответствии с задачами конкретного исследования и вероятность выводов по результатам наблюдения.

В целом формула предельной ошибки выборочной средней величины позволяет определять:

‣‣‣ величину возможных отклонений показателей генеральной совокупности от показателей выборочной совокупности;

‣‣‣ необходимую численность выборки, обеспечивающую требуемую точность, при которой пределы возможной ошибки не превысят некоторой заданной величины;

‣‣‣ вероятность того, что в проведенной выборке ошибка будет иметь заданный предел.

Распределе́ние Стью́дента в теории вероятностей - это однопараметрическое семейство абсолютно непрерывных распределений.

24.Ряды динамики (интервальные, моментные), смыкание рядов динамики.

Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.

Каждый динамический ряд содержит две составляющие:

1) показатели периодов времени (годы, кварталы, месяцы, дни или даты);

2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда .

Уровни ряда выражаются как абсолютными, так и средними или относительными величинами. Учитывая зависимость отхарактера показателей строят динамические ряды абсолютных, относительных и средних величин. Ряды динамики из относительных и средних величин строят на базе производных рядов абсолютных величин. Различают интервальные и моментные ряды динамики.

Динамический интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объём явления за более длительный период, или так называемые накопленные итоги.

Динамический моментный ряд отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются.

Важнейшим условием правильного построения динамических рядов является сопоставимость уровней рядов , относящихся к различным периодам. Уровни должны быть представлены в однородных величинах, должна иметь место одинаковая полнота охвата различных частей явления.

Для того, чтобы избежать искажения реальной динамики, в статистическом исследовании проводятся предварительные расчёты (смыкание рядов динамики), которые предшествуют статистическому анализу динамических рядов. Под смыканием рядов динамики принято понимать объединение в один ряд двух и более рядов, уровни которых рассчитаны по разной методологии или не соответствуют территориальным границам и т.д. Смыкание рядов динамики может предполагать также приведение абсолютных уровней рядов динамики к общему основанию, что нивелирует несопоставимость уровней рядов динамики.

25.Понятие сопоставимости рядов динамики, коэффициенты, темпы роста и прироста.

Ряды динамики - это ряды статистических показателей, характеризующих развитие явлений природы и общества во времени. Публикуемые Госкомстатом России статистические сборники содержат большое количество рядов динамики в табличной форме. Ряды динамики позволяют выявить закономерности развития изучаемых явлений.

Ряды динамики содержат два вида показателей. Показатели времени (годы, кварталы, месяцы и др.) или моменты времени (на начало года, на начало каждого месяца и т.п.). Показатели уровней ряда . Показатели уровней рядов динамики бывают выражены абсолютными величинами (производство продукта в тоннах или рублях), относительными величинами (удельный вес городского населения в %) и средними величинами (средняя зарплата работников отрасли по годам и т. п.). В табличной форме ряд динамики содержит два столбца или две строки.

Правильное построение рядов динамики предполагает выполнение ряда требований:

все показатели ряда динамики должны быть научно обоснованными, достоверными;
показатели ряда динамики должны быть сопоставимы по времени, ᴛ.ᴇ. должны быть исчислены за одинаковые периоды времени или на одинаковые даты;
показатели ряда динамики должны быть сопоставимы по территории;
показатели ряда динамики должны быть сопоставимы по содержанию, ᴛ.ᴇ. исчислены по единой методологии, одинаковым способом;
показатели ряда динамики должны быть сопоставимы по кругу учитываемых хозяйств. Все показатели ряда динамики должны быть приведены в одних и тех же единицах измерения.

Статистические показатели могут характеризовать либо результаты изучаемого процесса за период времени, либо состояние изучаемого явления на определенный момент времени, ᴛ.ᴇ. показатели бывают интервальными (периодическими) и моментными. Соответственно первоначально ряды динамики бывают либо интервальными, либо моментными. Моментные ряды динамики в свою очередь бывают с равными и неравными промежутками времени.

Первоначальные ряды динамики бывают преобразованы в ряд средних величин и ряд относительных величин (цепной и базисный). Такие ряды динамики называют производными рядами динамики.

Методика расчета среднего уровня в рядах динамики различна, обусловлена видом ряда динамики. На примерах рассмотрим виды рядов динамики и формулы для расчета среднего уровня.

Абсолютные приросты (Δy ) показывают, на сколько единиц изменился последующий уровень ряда по сравнению с предыдущим (гр.3. - цепные абсолютные приросты) или по сравнению с начальным уровнем (гр.4. - базисные абсолютные приросты). Формулы расчета можно записать следующим образом:

При уменьшении абсолютных значений ряда будет соответственно "уменьшение", "снижение".

Показатели абсолютного прироста свидетельствуют о том, что, к примеру, в 1998 ᴦ. производство продукта "А" увеличилось по сравнению с 1997 ᴦ. на 4 тыс. т, а по сравнению с 1994 ᴦ. - на 34 тыс. т.; по остальным годам см. табл. 11.5 гр.
Размещено на реф.рф
3 и 4.

Коэффициент роста показывает, во сколько раз изменился уровень ряда по сравнению с предыдущим (гр.5 - цепные коэффициенты роста или снижения) или по сравнению с начальным уровнем (гр.6 - базисные коэффициенты роста или снижения). Формулы расчета можно записать следующим образом:

Темпы роста показывают, сколько процентов составляет последующий уровень ряда по сравнению с предыдущим (гр.7 - цепные темпы роста) или по сравнению с начальным уровнем (гр.8 - базисные темпы роста). Формулы расчета можно записать следующим образом:

Так, к примеру, в 1997 ᴦ. объём производства продукта "А" по сравнению с 1996 ᴦ. составил 105,5 % (

Темпы прироста показывают, на сколько процентов увеличился уровень отчетного периода по сравнению с предыдущим (гр.9- цепные темпы прироста) или по сравнению с начальным уровнем (гр.10- базисные темпы прироста). Формулы расчета можно записать следующим образом:

Т пр = Т р - 100% или Т пр = абсолютный прирост / уровень предшествующего периода * 100%

Так, к примеру, в 1996 ᴦ. по сравнению с 1995 ᴦ. продукта "А" произведено больше на 3,8 % (103,8 %- 100%) или (8:210)х100%, а по сравнению с 1994 ᴦ. - на 9% (109% - 100%).

В случае если абсолютные уровни в ряду уменьшаются, то темп будет меньше 100% и соответственно будет темп снижения (темп прироста со знаком минус).

Абсолютное значение 1% прироста (гр.
Размещено на реф.рф
11) показывает, сколько единиц нужно произвести в данном периоде, чтобы уровень предыдущего периода возрос на 1 %. В нашем примере, в 1995 ᴦ. нужно было произвести 2,0 тыс. т., а в 1998 ᴦ. - 2,3 тыс. т., ᴛ.ᴇ. значительно больше.

Определить величину абсолютного значения 1% прироста можно двумя способами:

§ уровень предшествующего периода разделить на 100;

§ цепные абсолютные приросты разделить на соответствующие цепные темпы прироста.

Абсолютное значение 1% прироста =

В динамике, особенно за длительный период, важен совместный анализ темпов прироста с содержанием каждого процента прироста или снижения.

Заметим, что рассмотренная методика анализа рядов динамики применима как для рядов динамики, уровни которых выражены абсолютными величинами (т, тыс. руб., число работников и т.д.), так и для рядов динамики, уровни которых выражены относительными показателями (% брака, % зольности угля и др.) или средними величинами (средняя урожайность в ц/га, средняя зарплата и т.п.).

Наряду с рассмотренными аналитическими показателями, исчисляемыми за каждый год в сравнении с предшествующим или начальным уровнем, при анализе рядов динамики крайне важно исчислить средние за период аналитические показатели: средний уровень ряда, средний годовой абсолютный прирост (уменьшение) и средний годовой темп роста и темп прироста.

Методы расчета среднего уровня ряда динамики были рассмотрены выше. В рассматриваемом нами интервальном ряду динамики средний уровень ряда исчисляется по формуле средней арифметической простой:

Среднегодовой объём производства продукта за 1994- 1998 гᴦ. составил 218,4 тыс. т.

Среднегодовой абсолютный прирост исчисляется также по формуле средней арифметической

Среднее квадратическое отклонение - понятие и виды. Классификация и особенности категории "Среднее квадратическое отклонение" 2017, 2018.

Ответы на экзаменационные вопросы по общественному здоровью и здравоохранению.
1. Общественное здоровье и здравоохранение как наука и область практической деятельности. Основные задачи. Объект, предмет изучения. Методы.
2. Здравоохранение. Определение. История развития здравоохранения. Современные системы здравоохранения, их характеристика.
3. Государственная политика в области охраны здоровья населения (Закон Республики Беларусь "о здравоохранении"). Организационные принципы государственной системы здравоохранения.
4. Страховая и частная формы здравоохранения.
5. Профилактика, определение, принципы, современные проблемы. Виды, уровни, направления профилактики.
6. Национальные программы профилактики. Роль их в укреплении здоровья населения.
7. Врачебная этика и деонтология. Определение понятия. Современные проблемы врачебной этики и деонтологии, характеристика.
8. Здоровый образ жизни, определение понятия. Социальные и медицинские аспекты здорового образа жизни (зож).
9. Гигиеническое обучение и воспитание, определение, основные принципы. Методы и средства гигиенического обучения и воспитания. Требования к лекции, санитарному бюллетеню.
10. Здоровье населения, факторы, влияющие на здоровье населения. Формула здоровья. Показатели, характеризующие общественное здоровье. Схема анализа.
11. Демография как наука, определение, содержание. Значение демографических данных для здравоохранения.
12. Статика населения, методика изучения. Переписи населения. Типы возрастных структур населения.
13. Механическое движение населения. Характеристика миграционных процессов, влияние их на показатели здоровья населения.
14. Рождаемость как медико-социальная проблема. Методика вычисления показателей. Уровни рождаемости по данным воз. Современные тенденции.
15. Специальные показатели рождаемости (показатели фертильности). Воспроизводство населения, типы воспроизводства. Показатели, методика вычисления.
16. Смертность населения как медико-социальная проблема. Методика изучения, показатели. Уровни общей смертности по данным воз. Современные тенденции.
17. Младенческая смертность как медико-социальная проблема. Факторы, определяющие ее уровень.
18. Материнская и перинатальная смертность, основные причины. Показатели, методика вычисления.
19. Естественное движение населения, факторы на него влияющие. Показатели, методика вычисления. Основные закономерности естественного движения в Беларуси.
20. Планирование семьи. Определение. Современные проблемы. Медицинские организации и службы планирования семьи в рб.
21. Заболеваемость как медико-социальная проблема. Современные тенденции и особенности в Республике Беларусь.
22. Медико-социальные аспекты нервно-психического здоровья населения. Организация психоневрологической помощи
23. Алкоголизм и наркомания как медико-социальная проблема
24. Болезни системы кровообращения как медико-социальная проблема. Факторы риска. Направления профилактики. Организация кардиологической помощи.
25. Злокачественные новообразования как медико-социальная проблема. Основные направления профилактики. Организация онкологической помощи.
26. Международная статистическая классификация болезней. Принципы построения, порядок пользования. Значение ее в изучении заболеваемости и смертности населения.
27. Методы изучения заболеваемости населения, их сравнительная характеристика.
Методика изучения общей и первичной заболеваемости
Показатели общей и первичной заболеваемости.
Показатели инфекционной заболеваемости.
Основные показатели, характеризующие важнейшую неэпидемическую заболеваемость.
Основные показатели "госпитализированной" заболеваемости:
4) Заболевания с временной утратой трудоспособности (вопрос 30)
Основные показатели для анализа заболеваемости с вут.
31. Изучение заболеваемости по данным профилактических осмотров населения, виды профилактических осмотров, порядок проведения. Группы здоровья. Понятие «патологическая пораженность».
32. Заболеваемость по данным о причинах смерти. Методика изучения, показатели. Врачебное свидетельство о смерти.
Основные показатели заболеваемости по данным о причинах смерти:
33. Инвалидность как медико-социальная проблема Определение понятия, показатели. Тенденции инвалидности в Республике Беларусь.
Тенденции инвалидности в рб.
34. Первичная медико-санитарная помощь (пмсп), определение, содержание, роль и место в системе медицинского обслуживания населения. Основные функции.
35. Основные принципы первичной медико-санитарной помощи. Медицинские организации первичной медико-санитарной помощи.
36. Организация медицинской помощи, предоставляемой населению амбулаторно. Основные принципы. Учреждения.
37. Организация медицинской помощи в условиях стационара. Учреждения. Показатели обеспеченности стационарной помощью.
38. Виды медицинской помощи. Организация специализированной медицинской помощи населению. Центры специализированной медицинской помощи, их задачи.
39. Основные направления совершенствования стационарной и специализированной помощи в Республике Беларусь.
40. Охрана здоровья женщин и детей в Республике Беларусь. Управление. Медицинские организации.
41. Современные проблемы охраны здоровья женщин. Организация акушерско-гинекологической помощи в Республике Беларусь.
42. Организация лечебно-профилактической помощи детскому населению. Ведущие проблемы охраны здоровья детей.
43. Организация охраны здоровья сельского населения, основные принципы оказания медицинской помощи сельским жителям. Этапы. Организации.
II этап – территориальное медицинское объединение (тмо).
III этап – областная больница и медицинские учреждения области.
45. Медико-социальная экспертиза (мсэ), определение, содержание, основные понятия.
46. Реабилитация, определение, виды. Закон Республики Беларусь «о предупреждении инвалидности и реабилитации инвалидов».
47. Медицинская реабилитация: определение понятия, этапы, принципы. Служба медицинской реабилитации в Республике Беларусь.
48. Городская поликлиника, структура, задачи, управление. Основные показатели деятельности поликлиники.
Основные показатели деятельности поликлиники.
49. Участковый принцип организации амбулаторной помощи населению. Виды участков. Территориальный терапевтический участок. Нормативы. Содержание работы участкового врача-терапевта.
Организация работы участкового терапевта.
50. Кабинет инфекционных заболеваний поликлиники. Разделы и методы работы врача кабинета инфекционных заболеваний.
52. Основные показатели, характеризующие качество и эффективность диспансерного наблюдения. Методика их вычисления.
53. Отделение медицинской реабилитации (омр) поликлиники. Структура, задачи. Порядок направления больных в омр.
54. Детская поликлиника, структура, задачи, разделы работы. Особенности оказания медицинской помощи детям в амбулаторных условиях.
55. Основные разделы работы участкового педиатра. Содержание лечебно-профилактической работы. Связь в работе с другими лечебно-профилактическими учреждениями. Документация.
56. Содержание профилактической работы участкового врача-педиатра. Организация патронажного наблюдения за новорожденными.
57. Структура, организация, содержание работы женской консультации. Показатели работы по обслуживанию беременных женщин. Документация.
58. Родильный дом, структура, организация работы, управление. Показатели деятельности родильного дома. Документация.
59. Городская больница, ее задачи, структура, основные показатели деятельности. Документация.
60. Организация работы приемного отделения больницы. Документация. Мероприятия по профилактике внутрибольничных инфекций. Лечебно-охранительный режим.
Раздел 1. Сведения о подразделениях, установках лечебно-профилактической организации.
Раздел 2. Штаты лечебно-профилактической организации на конец отчетного года.
Раздел 3. Работа врачей поликлиники (амбулаторий), диспансера, консультации.
Раздел 4. Профилактические медицинские осмотры и работа стоматологических (зубоврачебных) и хирургических кабинетов лечебно-профилактической организации.
Раздел 5. Работа лечебно-вспомогательных отделений (кабинетов).
Раздел 6. Работа диагностических отделений.
62. Годовой отчет о деятельности стационара (ф. 14), порядок составления, структура. Основные показатели деятельности стационара.
Раздел 1. Состав больных в стационаре и исходы их лечения
Раздел 2. Состав больных новорожденных, переведенных в другие стационары в возрасте 0-6 суток и исходы их лечения
Раздел 3. Коечный фонд и его использование
Раздел 4. Хирургическая работа стационара
63. Отчет о медицинской помощи беременным, роженицам и родильницам (ф. 32), структура. Основные показатели.
Раздел I. Деятельность женской консультации.
Раздел II. Родовспоможение в стационаре
Раздел III. Материнская смертность
Раздел IV. Сведения о родившихся
64. Медико-генетическое консультирование, основные учреждения. Его роль в профилактике перинатальной и младенческой смертности.
65. Медицинская статистика, ее разделы, задачи. Роль статистического метода в изучении здоровья населения и деятельности системы здравоохранения.
66. Статистическая совокупность. Определение, виды, свойства. Особенности проведения статистического исследования на выборочной совокупности.
67. Выборочная совокупность, требования, предъявляемые к ней. Принцип и способы формирования выборочной совокупности.
68. Единица наблюдения. Определение, характеристика учетных признаков.
69. Организация статистического исследования. Характеристика этапов.
70. Содержание плана и программы статистического исследования. Виды планов статистического исследования. Программа наблюдения.
71. Статистическое наблюдение. Сплошное и несплошное статистическое исследование. Виды несплошного статистического исследования.
72. Статистическое наблюдение (сбор материалов). Ошибки статистического наблюдения.
73. Статистическая группировка и сводка. Типологическая и вариационная группировка.
74. Статистические таблицы, виды, требования к построению.

81. Среднее квадратическое отклонение, методика расчета, применение.

Приближенный метод оценки колеблемости вариационного ряда - определение лимита и амплитуды, однако не учитывают значений вариант внутри ряда. Основной общепринятой мерой колеблемости количественного признака в пределах вариационного ряда является среднее квадратическое отклонение (σ - сигма) . Чем больше среднее квадратическое отклонение, тем степень колеблемости данного ряда выше.

Методика расчета среднего квадратического отклонения включает следующие этапы:

1. Находят среднюю арифметическую величину (Μ).

2. Определяют отклонения отдельных вариант от средней арифметической (d=V-M). В медицинской статистике отклонения от средней обозначаются как d (deviate). Сумма всех отклонений равняется нулю.

3. Возводят каждое отклонение в квадрат d 2 .

4. Перемножают квадраты отклонений на соответствующие частоты d 2 *p.

5. Находят сумму произведений (d 2 *p)

6. Вычисляют среднее квадратическое отклонение по формуле:

при n больше 30, или
при n меньше либо равно 30, где n - число всех вариант.

Значение среднего квадратичного отклонения:

1. Среднее квадратическое отклонение характеризует разброс вариант относительно средней величины (т.е. колеблемость вариационного ряда). Чем больше сигма, тем степень разнообразия данного ряда выше.

2. Среднее квадратичное отклонение используется для сравнительной оценки степени соответствия средней арифметической величины тому вариационному ряду, для которого она вычислена.

Вариации массовых явлений подчиняются закону нормального распределения. Кривая, отображающая это распределение, имеет вид плавной колоколообразной симметричной кривой (кривая Гаусса). Согласно теории вероятности в явлениях, подчиняющихся закону нормального распределения, между значениями средней арифметической и среднего квадратического отклонения существует строгая математическая зависимость. Теоретическое распределение вариант в однородном вариационном ряду подчиняется правилу трех сигм.

Если в системе прямоугольных координат на оси абсцисс отложить значения количественного признака (варианты), а на оси ординат - частоты встречаемости вариант в вариационном ряду, то по сторонам от средней арифметической равномерно располагаются варианты с большими и меньшими значениями.

Установлено, что при нормальном распределении признака:

68,3% значений вариант находится в пределах М1

95,5% значений вариант находится в пределах М2

99,7% значений вариант находится в пределах М3

3. Среднее квадратическое отлонение позволяет установить значения нормы для клинико-биологических показателей. В медицине интервал М1 обычно принимается за пределы нормы для изучаемого явления. Отклонение оцениваемой величины от средней арифметической больше, чем на 1 указывает на отклонение изучаемого параметра от нормы.

4. В медицине правило трех сигм применяется в педиатрии для индивидуальной оценки уровня физического развития детей (метод сигмальных отклонений), для разработки стандартов детской одежды

5. Среднее квадратическое отклонение необходимо для характеристики степени разнообразия изучаемого признака и вычисления ошибки средней арифметической величины.

Величина среднего квадратического отклонения обычно используется для сравнения колеблемости однотипных рядов. Если сравниваются два ряда с разными признаками (рост и масса тела, средняя длительность лечения в стационаре и больничная летальность и т.д.), то непосредственное сопоставление размеров сигм невозможно, т.к. среднеквадратическое отклонение - именованная величина, выраженная в абсолютных числах. В этих случаях применяют коэффициент вариации (Cv ) , представляющий собой относительную величину: процентное отношение среднего квадратического отклонения к средней арифметической.

Коэффициент вариации вычисляется по формуле:

Чем выше коэффициент вариации, тем большая изменчивость данного ряда. Считают, что коэффициент вариации свыше 30 % свидетельствует о качественной неоднородности совокупности.

Среднеквадрати́ческое отклоне́ние (синонимы: среднее квадрати́ческое отклоне́ние , среднеквадрати́чное отклоне́ние , квадрати́чное отклоне́ние ; близкие термины: станда́ртное отклоне́ние , станда́ртный разбро́с ) - в теории вероятностей и статистике наиболее распространённый показатель рассеивания значений случайной величины относительно её математического ожидания . При ограниченных массивах выборок значений вместо математического ожидания используется среднее арифметическое совокупности выборок.

Энциклопедичный YouTube

1 / 5
Среднеквадратическое отклонение измеряется в единицах измерения самой случайной величины и используется при расчёте стандартной ошибки среднего арифметического , при построении доверительных интервалов , при статистической проверке гипотез , при измерении линейной взаимосвязи между случайными величинами. Определяется как квадратный корень из дисперсии случайной величины .
Среднеквадратическое отклонение:
s = n n − 1 σ 2 = 1 n − 1 ∑ i = 1 n (x i − x ¯) 2 ; {\displaystyle s={\sqrt {{\frac {n}{n-1}}\sigma ^{2}}}={\sqrt {{\frac {1}{n-1}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}};}
- Примечание: Очень часто встречаются разночтения в названиях СКО (Среднеквадратического отклонения) и СТО (Стандартного отклонения) с их формулами. Например, в модуле numPy языка программирования Python функция std() описывается как "standart deviation", в то время как формула отражает СКО (деление на корень из выборки). В Excel же функция СТАНДОТКЛОН() другая (деление на корень из n-1).
Стандартное отклонение (оценка среднеквадратического отклонения случайной величины x относительно её математического ожидания на основе несмещённой оценки её дисперсии) s {\displaystyle s} :
σ = 1 n ∑ i = 1 n (x i − x ¯) 2 . {\displaystyle \sigma ={\sqrt {{\frac {1}{n}}\sum _{i=1}^{n}\left(x_{i}-{\bar {x}}\right)^{2}}}.}
где σ 2 {\displaystyle \sigma ^{2}} - дисперсия ; x i {\displaystyle x_{i}} - i -й элемент выборки; n {\displaystyle n} - объём выборки; - среднее арифметическое выборки:
x ¯ = 1 n ∑ i = 1 n x i = 1 n (x 1 + … + x n) . {\displaystyle {\bar {x}}={\frac {1}{n}}\sum _{i=1}^{n}x_{i}={\frac {1}{n}}(x_{1}+\ldots +x_{n}).}
Следует отметить, что обе оценки являются смещёнными. В общем случае несмещённую оценку построить невозможно. Однако оценка на основе оценки несмещённой дисперсии является состоятельной .
В соответствии с ГОСТ Р 8.736-2011 среднеквадратическое отклонение считается по второй формуле данного раздела. Пожалуйста, сверьте результаты.

Правило трёх сигм

Правило трёх сигм ( 3 σ {\displaystyle 3\sigma } ) - практически все значения нормально распределённой случайной величины лежат в интервале (x ¯ − 3 σ ; x ¯ + 3 σ) {\displaystyle \left({\bar {x}}-3\sigma ;{\bar {x}}+3\sigma \right)} . Более строго - приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале (при условии, что величина x ¯ {\displaystyle {\bar {x}}} истинная, а не полученная в результате обработки выборки).
Если же истинная величина x ¯ {\displaystyle {\bar {x}}} неизвестна, то следует пользоваться не σ {\displaystyle \sigma } , а s . Таким образом, правило трёх сигм преобразуется в правило трёх s .

Интерпретация величины среднеквадратического отклонения

Большее значение среднеквадратического отклонения показывает больший разброс значений в представленном множестве со средней величиной множества; меньшее значение, соответственно, показывает, что значения в множестве сгруппированы вокруг среднего значения.
Например, у нас есть три числовых множества: {0, 0, 14, 14}, {0, 6, 8, 14} и {6, 6, 8, 8}. У всех трёх множеств средние значения равны 7, а среднеквадратические отклонения, соответственно, равны 7, 5 и 1. У последнего множества среднеквадратическое отклонение маленькое, так как значения в множестве сгруппированы вокруг среднего значения; у первого множества самое большое значение среднеквадратического отклонения - значения внутри множества сильно расходятся со средним значением.
В общем смысле среднеквадратическое отклонение можно считать мерой неопределённости. К примеру, в физике среднеквадратическое отклонение используется для определения погрешности серии последовательных измерений какой-либо величины. Это значение очень важно для определения правдоподобности изучаемого явления в сравнении с предсказанным теорией значением: если среднее значение измерений сильно отличается от предсказанных теорией значений (большое значение среднеквадратического отклонения), то полученные значения или метод их получения следует перепроверить. отождествляется с риском портфеля.

Климат

Предположим, существуют два города с одинаковой средней максимальной дневной температурой, но один расположен на побережье, а другой на равнине. Известно, что в городах, расположенных на побережье, множество различных максимальных дневных температур меньше, чем у городов, расположенных внутри континента. Поэтому среднеквадратическое отклонение максимальных дневных температур у прибрежного города будет меньше, чем у второго города, несмотря на то, что среднее значение этой величины у них одинаковое, что на практике означает, что вероятность того, что максимальная температура воздуха каждого конкретного дня в году будет сильнее отличаться от среднего значения, выше у города, расположенного внутри континента.

Спорт

Предположим, что есть несколько футбольных команд, которые оцениваются по некоторому набору параметров, например, количеству забитых и пропущенных голов, голевых моментов и т. п. Наиболее вероятно, что лучшая в этой группе команда будет иметь лучшие значения по большему количеству параметров. Чем меньше у команды среднеквадратическое отклонение по каждому из представленных параметров, тем предсказуемее является результат команды, такие команды являются сбалансированными. С другой стороны, у команды с большим значением среднеквадратического отклонения сложно предсказать результат, что в свою очередь объясняется дисбалансом, например, сильной защитой, но слабым нападением.
Использование среднеквадратического отклонения параметров команды позволяет в той или иной мере предсказать результат матча двух команд, оценивая сильные и слабые стороны команд, а значит, и выбираемых способов борьбы.

Квадратный корень из дисперсии носит название среднего квадратического отклонения от средней, которое рассчитывается следующим образом:

Элементарное алгебраическое преобразование формулы среднего квадратического отклонения приводит ее к следующему виду:

Эта формула часто оказывается более удобной в практике расчетов.

Среднее квадратическое отклонение так же, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются конкретные значения признака от среднего их значения. Среднее квадратическое отклонение всегда больше среднего линейного отклонения. Между ними имеется такое соотношение:

Зная это соотношение, можно по известному показатели определить неизвестный, например, но (I рассчитать а и наоборот. Среднее квадратическое отклонение измеряет абсолютный размер колеблемости признака и выражается в тех же единицах измерения, что и значения признака (рублях, тоннах, годах и т.д.). Оно является абсолютной мерой вариации.

Для альтернативных признаков, например наличия или отсутствия высшего образования, страховки, формулы дисперсии и среднего квадратического отклонения такие:

Покажем расчет среднего квадратического отклонения по данным дискретного ряда, характеризующего распределение студентов одного из факультетов вуза по возрасту (табл. 6.2).

Таблица 6.2.

Результаты вспомогательных расчетов даны в графах 2-5 табл. 6.2.

Средний возраст студента, лет, определен по формуле средней арифметической взвешенной (графа 2):

Квадраты отклонения индивидуального возраста студента от среднего содержатся в графах 3-4, а произведения квадратов отклонений на соответствующие частоты - в графе 5.

Дисперсию возраста студентов, лет, найдем по формуле (6.2):

Тогда о = л/3,43 1,85 *ода, т.е. каждое конкретное значение возраста студента отклоняется от среднего значения на 1,85 года.

Коэффициент вариации

По своему абсолютному значению среднее квадратическое отклонение зависит не только от степени вариации признака, но и от абсолютных уровней вариантов и средней. Поэтому сравнивать средние квадратические отклонения вариационных рядов с различными средними уровнями непосредственно нельзя. Чтобы иметь возможность для такого сравнения, нужно найти удельный вес среднего отклонения (линейного или квадратического) в среднем арифметическом показателе, выраженном в процентах, т.е. рассчитать относительные показатели вариации.

Линейный коэффициент вариации вычисляют по формуле

Коэффициент вариации определяют по следующей формуле:

В коэффициентах вариации устраняется не только несопоставимость, связанная с различными единицами измерения изучаемого признака, но и несопоставимость, возникающая вследствие различий в величине средних арифметических. Кроме того, показатели вариации дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33%.

По данным табл. 6.2 и полученным выше результатам расчетов определим коэффициент вариации, %, по формуле (6.3):

Если коэффициент вариации превышает 33%, то это свидетельствует о неоднородности изучаемой совокупности. Полученное в пашем случае значение говорит о том, что совокупность студентов по возрасту однородна по своему составу. Таким образом, важная функция обобщающих показателей вариации - оценка надежности средних. Чем меньше с1, а2 и V, тем однороднее полученная совокупность явлений и надежнее полученная средняя. Согласно рассматриваемому математической статистикой "правилу трех сигм" в нормально распределенных или близких к ним рядах отклонения от средней арифметической, не превосходящие ±3ст, встречаются в 997 случаях из 1000. Таким образом, зная х и а, можно получить общее первоначальное представление о вариационном ряде. Если, например, средняя заработная плата работника по фирме составила 25 000 руб., а а равна 100 руб., то с вероятностью, близкой к достоверности, можно утверждать, что заработная плата работников фирмы колеблется в пределах (25 000 ± ± 3 х 100) т.е. от 24 700 до 25 300 руб.