Главная » Страховая » Как определить возможные пределы. Определение конечного предела последовательности

Как определить возможные пределы. Определение конечного предела последовательности

Для тех, кто хочет научиться находить пределы в данной статье мы расскажем об этом. Не будем углубляться в теорию, обычно её дают на лекциях преподаватели. Так что "скучная теория" должна быть у Вас законспектирована в тетрадках. Если этого нет, то почитать можно учебники взятые в библиотеке учебного заведения или на других интернет-ресурсах.

Итак, понятие предела достаточно важно в изучении курса высшей математики, особенно когда вы столкнетесь с интегральным исчислением и поймёте связь между пределом и интегралом. В текущем материале будут рассмотрены простые примеры, а также способы их решения.

Примеры решений

Пример 1
Вычислить а) $ \lim_{x \to 0} \frac{1}{x} $; б)$ \lim_{x \to \infty} \frac{1}{x} $
Решение
а) $$ \lim \limits_{x \to 0} \frac{1}{x} = \infty $$ б)$$ \lim_{x \to \infty} \frac{1}{x} = 0 $$ Нам часто присылают эти пределы с просьбой помочь решить. Мы решили их выделить отдельным примером и пояснить, что данные пределы необходимо просто запомнить, как правило. Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!
Ответ
$$ \text{a)} \lim \limits_{x \to 0} \frac{1}{x} = \infty \text{ б)}\lim \limits_{x \to \infty} \frac{1}{x} = 0 $$

Что делать с неопределенностью вида: $ \bigg [\frac{0}{0} \bigg ] $

Пример 3
Решить $ \lim \limits_{x \to -1} \frac{x^2-1}{x+1} $
Решение
Как всегда начинаем с подстановки значения $ x $ в выражение, стоящее под знаком предела. $$ \lim \limits_{x \to -1} \frac{x^2-1}{x+1} = \frac{(-1)^2-1}{-1+1}=\frac{0}{0} $$ Что теперь дальше? Что же должно получиться в итоге? Так как это неопределенность, то это ещё не ответ и продолжаем вычисление. Так как в числители у нас многочлен, то разложим его на множители, помощью знакомой всем формулы ещё со школьной скамьи $$ a^2-b^2=(a-b)(a+b) $$. Вспомнили? Отлично! Теперь вперед и с песней применять её :) Получаем, что числитель $ x^2-1=(x-1)(x+1) $ Продолжаем решать учитывая вышеприведенное преобразование: $$ \lim \limits_{x \to -1}\frac{x^2-1}{x+1} = \lim \limits_{x \to -1}\frac{(x-1)(x+1)}{x+1} = $$ $$ = \lim \limits_{x \to -1}(x-1)=-1-1=-2 $$
Ответ
$$ \lim \limits_{x \to -1} \frac{x^2-1}{x+1} = -2 $$

Устремим предел в последних двух примерах к бесконечности и рассмотрим неопределенность: $ \bigg [\frac{\infty}{\infty} \bigg ] $

Пример 5
Вычислить $ \lim \limits_{x \to \infty} \frac{x^2-1}{x+1} $
Решение
$ \lim \limits_{x \to \infty} \frac{x^2-1}{x+1} = \frac{\infty}{\infty} $ Что же делать? Как быть? Не стоит паниковать, потому что невозможное - возможно. Нужно вынести за скобки и в числителе и в знаменателе икс, а потом его сократить. После этого предел попытаться вычислить. Пробуем... $$ \lim \limits_{x \to \infty} \frac{x^2-1}{x+1} =\lim \limits_{x \to \infty} \frac{x^2(1-\frac{1}{x^2})}{x(1+\frac{1}{x})} = $$ $$ = \lim \limits_{x \to \infty} \frac{x(1-\frac{1}{x^2})}{(1+\frac{1}{x})} = $$ Используя определение из примера 2 и подставляя в место х бесконечность получаем: $$ = \frac{\infty(1-\frac{1}{\infty})}{(1+\frac{1}{\infty})} = \frac{\infty \cdot 1}{1+0} = \frac{\infty}{1} = \infty $$
Ответ
$$ \lim \limits_{x \to \infty} \frac{x^2-1}{x+1} = \infty $$

Алгоритм вычисления лимитов

Итак, давайте кратко подведем итог разобранным примерам и составим алгоритм решения пределов:

Подставить точку х в выражение, следующее после знака предела. Если получается определенное число, либо бесконечность, то предел решен полностью. В противном случае имеем неопределенность: "ноль делить на ноль" или "бесконечность делить на бесконечность" и переходим к следующим пунктам инструкции.
Чтобы устранить неопределенность "ноль делить на ноль" нужно разложить числитель и знаменатель на множители. Сократить подобные. Подставить точку х в выражение, стоящее под знаком предела.
Если неопределенность "бесконечность делить на бесконечность", тогда выносим и в числителе, и в знаменателе x наибольшей степени. Сокращаем иксы. Подставляем значения икса из под предела в оставшееся выражение.

В этой статье Вы ознакомились с основами решения пределов, часто используемых в курсе Математического анализа. Конечно же это не все типы задач, предлагающихся экзаменаторами, а только простейшие пределы. В следующих статьях поговорим о других типах заданий, но сперва необходимо усвоить этот урок, чтобы двигаться далее. Обсудим, что делать, если есть корни, степени, изучим бесконечно малые эквивалентные функции, замечательные пределы, правило Лопиталя.

Если у Вас не получается самостоятельно решить пределы, то не паникуйте. Мы всегда рады помочь!

Сегодня на уроке мы разберём строгое определение последовательности и строгое определение предела функции , а также научимся решать соответствующие задачи теоретического характера. Статья предназначена, прежде всего, для студентов 1-го курса естественнонаучных и инженерно-технических специальностей, которые начали изучать теорию математического анализа, и столкнулись с трудностями в плане понимания этого раздела высшей математики. Кроме того, материал вполне доступен и учащимся старших классов.

За годы существования сайта я получил недобрый десяток писем примерно такого содержания: «Плохо понимаю математический анализ, что делать?», «Совсем не понимаю матан, думаю бросить учёбу» и т.п. И действительно, именно матан часто прореживает студенческую группу после первой же сессии. Почему так обстоят дела? Потому что предмет немыслимо сложен? Вовсе нет! Теория математического анализа не столь трудна, сколько своеобразна . И её нужно принять и полюбить такой, какая она есть =)

Начнём с самого тяжёлого случая. Первое и главное – не надо бросать учёбу. Поймите правильно, бросить, оно всегда успеется;-) Безусловно, если через год-два от выбранной специальности будет тошнить, тогда да – следует задуматься (а не пороть горячку!) о смене деятельности. Но пока стОит продолжить. И, пожалуйста, забудьте фразу «Ничего не понимаю» – так не бывает, чтобы СОВСЕМ ничего не понимать.

Что делать, если с теорией плохо? Это, кстати, касается не только математического анализа. Если с теорией плохо, то сначала нужно СЕРЬЁЗНО налечь на практику. При этом решаются сразу две стратегические задачи:

– Во-первых, значительная доля теоретических знаний появилась благодаря практике. И поэтому многие люди понимают теорию через… – всё верно! Нет-нет, вы не о том подумали =)

– И, во-вторых, практические навыки с большой вероятностью «вытянут» вас на экзамене, даже если…, но не будем так настраиваться! Всё реально и всё реально «поднять» в достаточно короткие сроки. Математический анализ – это мой любимый раздел высшей математики, и поэтому я просто не мог не протянуть вам ноги руку помощи:

В начале 1-го семестра обычно проходят пределы последовательностей и пределы функций. Не понимаете, что это такое и не знаете, как их решать? Начните со статьи Пределы функций , в которой «на пальцах» рассмотрено само понятие и разобраны простейшие примеры. Далее проработайте другие уроки по теме, в том числе урок о пределах последовательностей , на котором я фактически уже сформулировал строгое определение.

Какие значки помимо знаков неравенств и модуля вы знаете?

– длинная вертикальная палка читается так: «такое, что», «такая, что», «такой, что» либо «такие, что» , в нашем случае, очевидно, речь идёт о номере – поэтому «такой, что»;

– для всех «эн», бОльших чем ;

– знак модуля означает расстояние , т.е. эта запись сообщает нам о том, что расстояние между значениями меньше эпсилон.

Ну как, убийственно сложно? =)

После освоения практики жду вас в следующем параграфе:

И в самом деле, немного порассуждаем – как сформулировать строгое определение последовательности? …Первое, что приходит на ум в свете практического занятия : «предел последовательности – это число, к которому бесконечно близко приближаются члены последовательности».

Хорошо, распишем последовательность :

Нетрудно уловить, что подпоследовательность бесконечно близко приближаются к числу –1, а члены с чётными номерами – к «единице».

А может быть предела два? Но тогда почему у какой-нибудь последовательности их не может быть десять или двадцать? Так можно далеко зайти. В этой связи логично считать, что если у последовательности существует предел, то он единственный .

Примечание : у последовательности нет предела, однако из неё можно выделить две подпоследовательности (см. выше), у каждой из которых существует свой предел.

Таким образом, высказанное выше определение оказывается несостоятельным. Да, оно работает для случаев вроде (чем я не совсем корректно пользовался в упрощённых объяснениях практических примеров) , но сейчас нам нужно отыскать строгое определение.

Попытка вторая: «предел последовательности – это число, к которому приближаются ВСЕ члены последовательности, за исключением, разве что их конечного количества». Вот это уже ближе к истине, но всё равно не совсем точно. Так, например, у последовательности половина членов вовсе не приближается к нулю – они ему просто-напросто равны =) К слову, «мигалка» вообще принимает два фиксированных значения.

Формулировку нетрудно уточнить, но тогда возникает другой вопрос: как записать определение в математических знаках? Научный мир долго бился над этой проблемой, пока ситуацию не разрешил известный маэстро , который, по существу, и оформил классический матанализ во всей его строгости. Коши предложил оперировать окрестностями , чем значительно продвинул теорию.

Рассмотрим некоторую точку и её произвольную -окрестность:

Значение «эпсилон» всегда положительно, и, более того, мы вправе выбрать его самостоятельно . Предположим, что в данной окрестности находится множество членов (не обязательно все) некоторой последовательности . Как записать тот факт, что, например десятый член попал в окрестность? Пусть он находится в правой её части. Тогда расстояние между точками и должно быть меньше «эпсилон»: . Однако если «икс десятое» расположено левее точки «а», то разность будет отрицательна, и поэтому к ней нужно добавить знак модуля : .

Определение : число называется пределом последовательности, если для любой его окрестности (заранее выбранной) существует натуральный номер – ТАКОЙ, что ВСЕ члены последовательности с бОльшими номерами окажутся внутри окрестности:

Или короче: , если

Иными словами, какое бы малое значение «эпсилон» мы ни взяли, рано или поздно «бесконечный хвост» последовательности ПОЛНОСТЬЮ окажется в этой окрестности.

Так, например, «бесконечный хвост» последовательности ПОЛНОСТЬЮ зайдёт в любую сколь угодно малую -окрестность точки . Таким образом, это значение является пределом последовательности по определению. Напоминаю, что последовательность, предел которой равен нулю, называют бесконечно малой .

Следует отметить, что для последовательности уже нельзя сказать «бесконечный хвост зайдёт » – члены с нечётными номерами по факту равны нулю и «никуда не заходят» =) Именно поэтому в определении использован глагол «окажутся». И, разумеется, члены такой последовательности, как тоже «никуда не идут». Кстати, проверьте, будет ли число её пределом.

Теперь покажем, что у последовательности не существует предела. Рассмотрим, например, окрестность точки . Совершенно понятно, что нет такого номера, после которого ВСЕ члены окажутся в данной окрестности – нечётные члены всегда будут «выскакивать» к «минус единице». По аналогичной причине не существует предела и в точке .

Закрепим материал практикой:

Пример 1

Доказать что предел последовательности равен нулю. Указать номер , после которого, все члены последовательности гарантированно окажутся внутри любой сколь угодно малой -окрестности точки .

Примечание : у многих последовательностей искомый натуральный номер зависит от значения – отсюда и обозначение .

Решение : рассмотрим произвольную найдётся ли номер – такой, что ВСЕ члены с бОльшими номерами окажутся внутри этой окрестности:

Чтобы показать существование искомого номера , выразим через .

Так как при любом значении «эн» , то знак модуля можно убрать:

Используем «школьные» действия с неравенствами, которые я повторял на уроках Линейные неравенства и Область определения функции . При этом важным обстоятельством является то, что «эпсилон» и «эн» положительны:

Поскольку слева речь идёт о натуральных номерах, а правая часть в общем случае дробна, то её нужно округлить:

Примечание : иногда для перестраховки справа добавляют единицу, но на самом деле это излишество. Условно говоря, если и мы ослабим результат округлением в меньшую сторону , то ближайший подходящий номер («тройка») всё равно будет удовлетворять первоначальному неравенству.

А теперь смотрим на неравенство и вспоминаем, что изначально мы рассматривали произвольную -окрестность, т.е. «эпсилон» может быть равно любому положительному числу.

Вывод : для любой сколько угодно малой -окрестности точки нашлось значение . Таким образом, число является пределом последовательности по определению. Что и требовалось доказать .

К слову, из полученного результата хорошо просматривается естественная закономерность: чем меньше -окрестность – тем больше номер , после которого ВСЕ члены последовательности окажутся в данной окрестности. Но каким бы малым ни было «эпсилон» – внутри всегда будет «бесконечный хвост», а снаружи – пусть даже большое, однако конечное число членов.

Как впечатления? =) Согласен, что странновато. Но строго! Пожалуйста, перечитайте и осмыслите всё ещё раз.

Рассмотрим аналогичный пример и познакомимся с другими техническими приёмами:

Пример 2

Решение : по определению последовательности нужно доказать, что (проговариваем вслух!!!) .

Рассмотрим произвольную -окрестность точки и проверим, существует ли натуральный номер – такой, что для всех бОльших номеров выполнено неравенство:

Чтобы показать существование такого , нужно выразить «эн» через «эпсилон». Упрощаем выражение под знаком модуля:

Модуль уничтожает знак «минус»:

Знаменатель положителен при любом «эн», следовательно, палки можно убрать:

Перетасовка:

Теперь надо бы извлечь квадратный корень, но загвоздка состоит в том, что при некоторых «эпсилон» правая часть будет отрицательной. Чтобы избежать этой неприятности усилим неравенство модулем:

Почему так можно сделать? Если, условно говоря, окажется, что , то подавно будет выполнено и условие . Модуль может только увеличить разыскиваемый номер , и это нас тоже устроит! Грубо говоря, если подходит сотый, то подойдёт и двухсотый! В соответствии с определением, нужно показать сам факт существования номера (хоть какого-то), после которого все члены последовательности окажутся в -окрестности. Кстати, именно поэтому нам не страшнО финальное округление правой части в бОльшую сторону.

Извлекаем корень:

И округляем результат:

Вывод : т.к. значение «эпсилон» выбиралось произвольно, то для любой сколько угодно малой -окрестности точки нашлось значение , такое, что для всех бОльших номеров выполнено неравенство . Таким образом, по определению. Что и требовалось доказать .

Советую особо разобраться в усилении и ослаблении неравенств – это типичные и очень распространённые приёмы математического анализа. Единственное, нужно следить за корректностью того или иного действия. Так, например, неравенство ни в коем случае нельзя ослаблять , вычитая, скажем, единицу:

Опять же условно: если номер точно подойдёт, то предыдущий может уже и не подойти.

Следующий пример для самостоятельного решения:

Пример 3

Используя определение последовательности, доказать, что

Краткое решение и ответ в конце урока.

Если последовательность бесконечно велика , то определение предела формулируется похожим образом: точка называется пределом последовательности, если для любого, сколь угодно большого числа существует номер , такой, что для всех бОльших номеров , будет выполнено неравенство . Число называют окрестностью точки «плюс бесконечность» :

Иными словами, какое бы большое значение мы ни взяли, «бесконечный хвост» последовательности обязательно зайдёт в -окрестность точки , оставив слева лишь конечное число членов.

Дежурный пример:

И сокращённая запись: , если

Для случая запишите определение самостоятельно. Правильная версия в конце урока.

После того, как вы «набили» руку на практических примерах и разобрались с определением предела последовательности, можно обратиться к литературе по математическому анализу и/или своей тетрадке с лекциями. Рекомендую закачать 1-й том Бохана (попроще – для заочников) и Фихтенгольца (более подробно и обстоятельно) . Из других авторов советую Пискунова, курс которого ориентирован на технические ВУЗы.

Попытайтесь добросовестно изучить теоремы, которые касаются предела последовательности, их доказательства, следствия. Поначалу теория может казаться «мутной», но это нормально – просто нужно привыкнуть. И многие даже войдут во вкус!

Строгое определение предела функции

Начнём с того же самого – как сформулировать данное понятие? Словесное определение предела функции формулируется значительно проще: «число является пределом функции , если при «икс», стремящемся к (и слева, и справа) , соответствующие значения функции стремятся к » (см. чертёж) . Всё вроде бы нормально, но слова словами, смысл смыслом, значок значком, а строгих математических обозначений маловато. И во втором параграфе мы познакомимся с двумя подходами к решению данного вопроса.

Пусть функция определена на некотором промежутке за исключением, возможно, точки . В учебной литературе общепринято считают, что функция там не определена:

Такой выбор подчёркивает суть предела функции : «икс» бесконечно близко приближается к , и соответствующие значения функции – бесконечно близко к . Иными словами, понятие предела подразумевает не «точный заход» в точки, а именно бесконечно близкое приближение , при этом не важно – определена ли функция в точке или нет.

Первое определение предела функции, что неудивительно, формулируется с помощью двух последовательностей. Во-первых, понятия родственные, и, во-вторых, пределы функций обычно изучают после пределов последовательностей.

Рассмотрим последовательность точек (на чертеже отсутствуют) , принадлежащих промежутку и отличных от , которая сходится к . Тогда соответствующие значения функции тоже образуют числовую последовательность, члены которой располагаются на оси ординат.

Предел функции по Гейне для любой последовательности точек (принадлежащих и отличных от ) , которая сходится к точке , соответствующая последовательность значений функции сходится к .

Эдуард Гейне – это немецкий математик. …И не надо тут ничего такого думать, гей в Европе всего лишь один – это Гей-Люссак =)

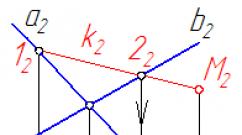
Второе определение предела соорудил… да-да, вы правы. Но сначала разберёмся в его конструкции. Рассмотрим произвольную -окрестность точки («чёрная» окрестность) . По мотивам предыдущего параграфа, запись означает, что некоторое значение функции находится внутри «эпсилон»-окрестности.

Теперь найдём -окрестность, которая соответствует заданной -окрестности (мысленно проводим чёрные пунктирные линии слева направо и затем сверху вниз) . Обратите внимание, что значение выбирается по длине меньшего отрезка, в данном случае – по длине более короткого левого отрезка. Более того, «малиновую» -окрестность точки можно даже уменьшить, поскольку в нижеследующем определении важен сам факт существования этой окрестности. И, аналогично, запись означает, что некоторое значение находится внутри «дельта»-окрестности.

Предел функции по Коши : число называется пределом функции в точке , если для любой заранее выбранной окрестности (сколь угодно малой) , существует -окрестность точки , ТАКАЯ , что: КАК ТОЛЬКО значения (принадлежащие ) входят в данную окрестность: (красные стрелки) – ТАК СРАЗУ соответствующие значения функции гарантированно зайдут в -окрестность: (синие стрелки) .

Должен предупредить, что в целях бОльшей доходчивости я немного сымпровизировал, поэтому не злоупотребляйте =)

Короткая запись: , если

В чём суть определения? Образно говоря, бесконечно уменьшая -окрестность, мы «сопровождаем» значения функции до своего предела, не оставляя им альтернативы приближаться куда-то ещё. Довольно необычно, но опять же строго! Чтобы как следует проникнуться идеей, перечитайте формулировку ещё раз.

! Внимание : если вам потребуется сформулировать только определение по Гейне или только определение по Коши , пожалуйста, не забывайте о существенном предварительном комментарии: «Рассмотрим функцию , которая определена на некотором промежутке за исключением, возможно, точки » . Я обозначил это единожды в самом начале и каждый раз не повторял.

Согласно соответствующей теореме математического анализа, определения по Гейне и по Коши эквивалентны, однако наиболее известен второй вариант (ещё бы!) , который также называют «предел на языке »:

Пример 4

Используя определение предела, доказать, что

Решение : функция определена на всей числовой прямой кроме точки . Используя определение , докажем существование предела в данной точке.

Примечание : величина «дельта»-окрестности зависит от «эпсилон», отсюда и обозначение

Рассмотрим произвольную -окрестность. Задача состоит в том, чтобы по этому значению проверить, существует ли -окрестность, ТАКАЯ , что из неравенства следует неравенство .

Предполагая, что , преобразуем последнее неравенство:
(разложили квадратный трёхчлен )

Члена последовательности.

Число а называется пределом последовательности {xn}, если для любого ε>0 существует номер n=n(ε), начиная с которого выполняется |xn-a |

Пример 2. Доказать, что в примера 1 число а=1 не является пределом последовательности предыдущего примера. Решение. Вновь упростите общий член последовательности. Возьмите ε=1 (это любое число >

Задачи непосредственного вычисления предела последовательности довольно однообразны. Все они содержат отношения полиномов относительно n или выражений относительно этих полиномов. Приступая к решению, вынесите за скобки (знак радикала) составляющую, находящуюся в старшей . Пусть для числителя исходного выражения это приведет к появлению множителя a^p, а для знаменателя b^q. Очевидно, что все оставшиеся слагаемые имеют вид С/(n-k) и стремятся к нулю при n>

Первый способ вычисления предела последовательности основан на ее определении. Правда следует запомнить, что путей непосредственного поиска предела он не дает, а позволяет лишь доказать, что какое-либо число а является (или не является) пределом.Пример 1. Доказать, что последовательность {xn}={(3n^2-2n-1)/(n^2-n-2)} имеет предел а=3.Решение. Проводите путем применения определения в обратном порядке. То есть справа налево. Предварительно проверьте – нет ли возможности упростить формулу для xn.хn =(3n^2+4n+2)/(n^2+3n22)=((3n+1)(n+1))/((n+2)(n+1))=)=(3n+1)/(n+2).Рассмотрите неравенство |(3n+1)/(n+2)-3|0 можно найти любое натуральное число nε, большее -2+5/ε.

Укажем не традиционный способ нахождения предела последовательности и бесконечных сумм. Будем использовать функциональные последовательности (их члены функции, определенные на некотором промежутке (a,b)).Пример 3. Найти сумму вида 1+1/2! +1/3! +…+1/n! +…=s .Решение. Любое число а^0=1. Положите 1=exp(0) и рассмотрите функциональную последовательность {1+x+x^2/2! +x^3/3! +…+x^/n!}, n=0,1,2,..,n… . Легко заметить, что записанный полином совпадает с многочленом Тейлора по степеням x, который в данном случае совпадает с exp(x). Возьмите х=1. Тогдаexp(1)=e=1+1+1/2! +1/3! +…+1/n! +…=1+s. Ответ s=e-1.

Совет 2: В какой последовательности смотреть фильмы Марвел про мстителей?

Вселенная «Марвел» основана на комиксах издательства Marvel, но далеко не все экранизации комиксов – часть киновселенной. В нее входит только снятое Marvel Studios или совместно с ней. Киновселенная «Марвел» разделена на фазы, каждый фильм в ней имеет свое место. Однако сериалы и короткометражки, являясь частью вселенной, в хронологии могут быть между фазами. Т.е. могут не принадлежать к конкретным частям киновселенной.

Сериалы Netflix и канала abc отличаются от вселенной «Марвел». У киновселенной есть две особенности:

каждый фильм наделен собственной историей;
глобальный сюжет переходит из одного фильма в другой, в итоге каждый из них двигает этот сюжет вперед.

Сериалы канала abc связаны с глобальным сюжетом киновселенной, но не продвигают, а только дополняют его. Сериалы Netflix - это и вовсе самостоятельные истории, со своим сюжетом и своим глобальным миром.

За годы существования вселенная «Марвел» разрослась, и продолжает расширяться. Поэтому разобраться с хронологией ее фильмов неподготовленному человеку сложно, ведь не каждому понятно, что нельзя смотреть «Железного человека 3» сразу после «Железного человека 2». А чтобы разобраться, надо изучить хронологию, которая включает три фазы.

Первая фаза:

Фильм «Железный человек», 2008 года. Эта картина закладывает фундамент и общий тон следующим экранизациям, ее действие происходит в 2010 году.
Фильм «Невероятный Халк», 2008 года. В этой экранизации зрители понимают, что истории двух разных героев случаются в одной вселенной, поскольку и в «Железном человеке», и в «Невероятном Халке» упомянут Щ.И.Т., программа «суперсолдат», встречается логотип StarkIndusries и т.д. Действие фильма разворачивается в 2011 году. Картина не продолжает историю фильма «Халк» 2003 года.
Фильм «Железный человек 2», 2010 года. Эта история - нечто вроде затравки к Мстителям, она вводит в сюжет Черную Вдову, дает много предпосылок к будущим проектам и рассказывает о новых проблемах Тони Старка, с которыми он столкнулся через год после первой части «Железного человека».
Фильм «Тор», 2011 года. Это тоже подготовка к Мстителям, и главная цель картины - познакомить зрителя с Тором и Локи. Действие сюжета происходит параллельно с историей «Невероятного Халка» и «Железного человека 2».
Фильм «Первый мститель», 2011 года. В нем рассказывают о Капитане Америка - первом супергерое Земли, который, как и Халк, появился из-за сыворотки «суперсолдат». Первая и последняя сцены фильма происходят в 2011 году, а основные действия - в период с 1943 по 1945 годы. В фильме появляется Тессеракт, один из шести Камней Бесконечности, и выясняется, что «отцом» Щ.И.Т.а была организация СНР (Стратегический Научный Резерв).
Короткометражка «Консультант», 2011 года. Здесь разъясняется финальная сцена фильма «Невероятный Халк».
Короткометражка «Забавный случай по пути к молоту Тора», 2011 года.
Фильм «Мстители», 2012 года. Действие сюжета разворачивается в 2012 году, когда Щ.И.Т. ради спасения мира объявляет «общий сбор».

Вторая фаза:

Фильм «Железный человек 3», 2013 года. Действие происходит зимой 2012 года, когда Тони Старк возвращается домой после «Битвы за Нью-Йорк», но его мучают кошмары. Спать он не может, и посвящает свое время созданию новых костюмов.
Сериал «Агенты Щ.И.Т.а», 2013 года.
Фильм «Тор 2: Царство Тьмы», 2013 года. В картине рассказывают, как Тор вернулся домой и обнаружил, что все девять миров погружены в хаос. И о том, как Тор наводил порядок.
Короткометражка «Да здравствует король», 2014 год. Это история о Треворе Слеттери, которая происходит после событий фильма «Железный человек 3».
Фильм «Первый мститель: Другая Война», 2014 года. Это история о Капитане Америка, который не может вернуться домой, потому ищет себе новое дело и становится агентом Щ.И.Т.а, работая в команде с Черной Вдовой. Фильм лучше смотреть между 16 и 17 сериями «Агентов Щ.И.Т.а».
Фильм «Стражи Галактики», 2014 год. Смотреть надо после 1 сезона сериала «Агенты Щ.И.Т.а». Это история о преступниках вне Земли, которые создали команду, чтобы остановить более опасного преступника Ронана, и не дать ему получить Камень Бесконечности.
Сериал «Агенты Щ.И.Т.а», второй сезон, 2014 год.
Сериал «Агент Картер», 2016 год. Это история о том, как Пегги Картер и дворецкий Эдвин Джарвис помогают Говарду Старку вернуть его доброе имя.
Фильм «Мстители: Эра Альтрона», 2015 года. В этой картине Мстители снова собрались, чтобы спасти мир, но этот раз они стали полноценной командой. Смотреть лучше между 19 и 20 сериями второго сезона «Агентов Щ.И.Т.а».
Фильм «Человек-Муравей», 2015 года. Смотреть после 2 сезона сериала «Агенты Щ.И.Т.а».

Третья фаза:

Фильм «Первый Мститель: Противостояние», 2016 года. После «Заковийского договора» Мстители обязаны подчиняться правительству, но это разбивает их на два лагеря: тех, кто за регистрацию, и тех, кто против нее.

Это все фильмы, которые уже вышли в прокат. Но не вся история. В третьей фазе планируется еще 14 фильмов, а потом - четвертая фаза.

Связанная статья

Этот математический калькулятор онлайн поможет вам если нужно вычислить предел функции . Программа решения пределов не просто даёт ответ задачи, она приводит подробное решение с пояснениями , т.е. отображает процесс вычисления предела.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.

Введите выражение функции
Вычислить предел

Обнаружено что не загрузились некоторые скрипты, необходимые для решения этой задачи, и программа может не работать.
Возможно у вас включен AdBlock.
В этом случае отключите его и обновите страницу.

У вас в браузере отключено выполнение JavaScript.
Чтобы решение появилось нужно включить JavaScript.
Вот инструкции, как включить JavaScript в вашем браузере .

Т.к. желающих решить задачу очень много, ваш запрос поставлен в очередь.
Через несколько секунд решение появится ниже.
Пожалуйста подождите сек...

Если вы заметили ошибку в решении , то об этом вы можете написать в Форме обратной связи .
Не забудте указать какую задачу вы решаете и что вводите в поля .

Наши игры, головоломки, эмуляторы:

Немного теории.

Предел функции при х->х 0

Пусть функция f(x) определена на некотором множестве X и пусть точка $x_0 \in X $ или $x_0 \notin X $

Возьмем из X последовательность точек, отличных от х 0:
x 1 , x 2 , x 3 , ..., x n , ... (1)
сходящуюся к х*. Значения функции в точках этой последовательности также образуют числовую последовательность
f(x 1), f(x 2), f(x 3), ..., f(x n), ... (2)
и можно ставить вопрос о существовании ее предела.

Определение . Число А называется пределом функции f(х) в точке х = х 0 (или при х -> x 0), если для любой сходящейся к x 0 последовательности (1) значений аргумента x, отличных от x 0 соответствующая последовательность (2) значений функции сходится к числу A.

$$ \lim_{x\to x_0}{ f(x)} = A $$

Функция f(x) может иметь в точке x 0 только один предел. Это следует из того, что последовательность
{f(x n)} имеет только один предел.

Существует другое определение предела функции.

Определение Число А называется пределом функции f(x) в точке х = x 0 , если для любого числа $\varepsilon > 0 $ существует число $\delta > 0 $ такое, что для всех $x \in X, \; x \neq x_0 $, удовлетворяющих неравенству $|x-x_0| Используя логические символы, это определение можно записать в виде
\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x \in X, \; x \neq x_0, \; |x-x_0| Отметим, что неравенства \(x \neq x_0, \; |x-x_0| Первое определение основано на понятии предела числовой последовательности, поэтому его часто называют определением «на языке последовательностей». Второе определение называют определением «на языке \(\varepsilon - \delta $».
Эти два определения предела функции эквивалентны и можно использовать любое из них в зависимости от того, какое более удобно при решении той или иной задачи.

Заметим, что определение предела функции «на языке последовательностей» называют также определением предела функции по Гейне, а определение предела функции «на языке $\varepsilon - \delta $» - определением предела функции по Коши.

Предел функции при x->x 0 - и при x->x 0 +

В дальнейшем будут использованы понятия односторонних пределов функции, которые определяются следующим образом.

Определение Число А называется правым (левым) пределом функции f(x) в точке x 0 , если для любой сходящейся к x 0 последовательности (1), элементы x n которой больше (меньше) x 0 , соответствующая последовательность (2) сходится к А.

Символически это записывается так:
$$ \lim_{x \to x_0+} f(x) = A \; \left(\lim_{x \to x_0-} f(x) = A \right) $$

Можно дать равносильное определение односторонних пределов функции «на языке $\varepsilon - \delta $»:

Определение число А называется правым (левым) пределом функции f(х) в точке x 0 , если для любого $\varepsilon > 0 $ существует $\delta > 0 $ такое, что для всех x, удовлетворяющих неравенствам \(x_0 Символические записи:

\((\forall \varepsilon > 0) (\exists \delta > 0) (\forall x, \; x_0

Приводятся формулировки основных теорем и свойств числовых последовательностей, имеющих предел. Содержится определение последовательности и ее предела. Рассмотрены арифметические действия с последовательностями, свойства, связанные с неравенствами, критерии сходимости, свойства бесконечно малых и бесконечно больших последовательностей.

Последовательности

Числовой последовательностью называется закон (правило), согласно которому, каждому натуральному числу ставится в соответствие число .
Число называют n-м членом или элементом последовательности.
Далее мы будем считать, что элементами последовательности являются действительные числа.

ограниченной , если существует такое число M , что для всех действительных n .

Верхней гранью последовательности называют наименьшее из чисел, ограничивающее последовательность сверху. То есть это такое число s , для которого для всех n и для любого , найдется такой элемент последовательности , превосходящий s′ : .

Нижней гранью последовательности называют наибольшее из чисел, ограничивающее последовательность снизу. То есть это такое число i , для которого для всех n и для любого , найдется такой элемент последовательности , меньший i′ : .

Верхнюю грань также называют точной верхней границей , а нижнюю грань - точной нижней границей . Понятия верхней и нижней граней справедливы не только к последовательностям, но и к любым множествам действительных чисел.

Определение предела последовательности

Число a называется пределом последовательности , если для любого положительного числа существует такое натуральное число N , зависящее от , что для всех натуральных выполняется неравенство
.
Предел последовательности обозначается так:
.
Или при .

С помощью логических символов существования и всеобщности определение предела можно записать следующим образом:
.

Открытый интервал (a - ε, a + ε) называют ε - окрестностью точки a .

Последовательность, у которой существует предел называется сходящейся последовательностью . Также говорят, что последовательность сходится к a . Последовательность, не имеющая предела, называется расходящейся .

Точка a не является пределом последовательности , если существует такое , что для любого натурального n существует такое натуральное m > n , что
.
.
Это означает, что можно выбрать такую ε - окрестностью точки a , за пределами которой будет находиться бесконечное число элементов последовательности.

Свойства конечных пределов последовательностей

Основные свойства

Точка a является пределом последовательности тогда и только тогда, когда за пределами любой окрестности этой точки находится конечное число элементов последовательности или пустое множество.

Если число a не является пределом последовательности , то существует такая окрестность точки a , за пределами которой находится бесконечное число элементов последовательности .

Теорема единственности предела числовой последовательности . Если последовательность имеет предел, то он единственный.

Если последовательность имеет конечный предел, то она ограничена .

Если каждый элемент последовательности равен одному и тому же числу C : , то эта последовательность имеет предел, равный числу C .

Если у последовательности добавить, отбросить или изменить первые m элементов , то это не повлияет на ее сходимость.

Доказательства основных свойств приведены на странице
Основные свойства конечных пределов последовательностей >>> .

Арифметические действия с пределами

Пусть существуют конечные пределы и последовательностей и . И пусть C - постоянная, то есть заданное число. Тогда
;
;
;
, если .
В случае частного предполагается, что для всех n .

Если , то .

Доказательства арифметических свойств приведены на странице
Арифметические свойства конечных пределов последовательностей >>> .

Свойства, связанные с неравенствами

Если и элементы последовательности, начиная с некоторого номера, удовлетворяют неравенству , то и предел a этой последовательности удовлетворяет неравенству .

Если и элементы последовательности, начиная с некоторого номера, принадлежат замкнутому интервалу (сегменту) , то и предел a также принадлежит этому интервалу: .

Если и и элементы последовательностей, начиная с некоторого номера, удовлетворяют неравенству , то .

Если и, начиная с некоторого номера, , то .
В частности, если, начиная с некоторого номера, , то
если , то ;
если , то .

Если и , то .

Пусть и . Если a < b , то найдется такое натуральное число N , что для всех n > N выполняется неравенство .

Доказательства свойств, связанных с неравенствами приведены на странице
Свойства пределов последовательностей, связанные с неравенствами >>> .

Бесконечно большая и бесконечно малая последовательности

Бесконечно малая последовательность

Последовательность называется бесконечно малой последовательностью , если ее предел равен нулю:
.

Сумма и разность конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Произведение ограниченной последовательности на бесконечно малую является бесконечно малой последовательностью.

Произведение конечного числа бесконечно малых последовательностей является бесконечно малой последовательностью.

Для того, чтобы последовательность имела предел a , необходимо и достаточно, чтобы , где - бесконечно малая последовательность.

Доказательства свойств бесконечно малых последовательностей приведены на странице
Бесконечно малые последовательности - определение и свойства >>> .

Бесконечно большая последовательность

Последовательность называется бесконечно большой последовательностью , если для любого положительного числа существует такое натуральное число N , зависящее от , что для всех натуральных выполняется неравенство
.
В этом случае пишут
.
Или при .
Говорят, что стремится к бесконечности.

Если , начиная с некоторого номера N , то
.
Если же , то
.

Если последовательность являются бесконечно большой, то, начиная с некоторого номера N , определена последовательность , которая является бесконечно малой. Если являются бесконечно малой последовательностью с отличными от нуля элементами, то последовательность является бесконечно большой.

Если последовательность бесконечно большая, а последовательность ограничена, то
.

Если абсолютные значения элементов последовательности ограничены снизу положительным числом (), а - бесконечно малая с неравными нулю элементами, то
.

Более подробно определение бесконечно большой последовательности с примерами приводится на странице
Определение бесконечно большой последовательности >>> .
Доказательства свойств бесконечно больших последовательностей приведены на странице
Свойства бесконечно больших последовательностей >>> .

Критерии сходимости последовательностей

Монотонные последовательности

Последовательность называется строго возрастающей , если для всех n выполняется неравенство:
.
Соответственно, для строго убывающей последовательности выполняется неравенство:
.
Для неубывающей :
.
Для невозрастающей :
.

Отсюда следует, что строго возрастающая последовательность также является неубывающей. Строго убывающая последовательность также является невозрастающей.

Последовательность называется монотонной , если она неубывающая или невозрастающая.

Монотонная последовательность ограничена, по крайней мере, с одной стороны значением . Неубывающая последовательность ограничена снизу: . Невозрастающая последовательность ограничена сверху: .

Теорема Вейерштрасса . Для того чтобы неубывающая (невозрастающая) последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной сверху (снизу ). Здесь M - некоторое число.

Поскольку любая неубывающая (невозрастающая) последовательность ограничена снизу (сверху), то теорему Вейерштрасса можно перефразировать следующим образом:

Для того чтобы монотонная последовательность имела конечный предел, необходимо и достаточно, чтобы она была ограниченной: .

Монотонная неограниченная последовательность имеет бесконечный предел, равный для неубывающей и для невозрастающей последовательности.

Доказательство теоремы Вейерштрасса приведено на странице
Теорема Вейерштрасса о пределе монотонной последовательности >>> .

Критерий Коши сходимости последовательности

Условие Коши . Последовательность удовлетворяет условию Коши, если для любого существует такое натуральное число , что для всех натуральных чисел n и m , удовлетворяющих условию , выполняется неравенство
.
Последовательности, удовлетворяющие условию Коши, также называют фундаментальными последовательностями .

Критерий Коши сходимости последовательности . Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она удовлетворяла условию Коши.

Доказательство критерия сходимости Коши приведено на странице
Критерий Коши сходимости последовательности >>> .

Подпоследовательности

Теорема Больцано - Вейерштрасса . Из любой ограниченной последовательности можно выделить сходящуюся подпоследовательность. А из любой неограниченной последовательности - бесконечно большую подпоследовательность, сходящуюся к или к .

Доказательство теоремы Больцано - Вейерштрасса приведено на странице
Теорема Больцано – Вейерштрасса >>> .

Определения, теоремы и свойства подпоследовательностей и частичных пределов рассмотрены на странице
Подпоследовательности и частичные пределы последовательностей >>>.

Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
В.А. Зорич. Математический анализ. Часть 1. Москва, 1997.
В.А. Ильин, Э.Г. Позняк. Основы математического анализа. Часть 1. Москва, 2005.

Просмотров