Чем ближе коэффициент корреляции к 1. Пример нахождения коэффициента корреляции

Целью корреляционного анализа является выявление оценки силы связи между случайными величинами (признаками), которые характеризует некоторый реальный процесс.
Задачи корреляционного анализа :
а) Измерение степени связности (тесноты, силы, строгости, интенсивности) двух и более явлений.
б) Отбор факторов, оказывающих наиболее существенное влияние на результативный признак, на основании измерения степени связности между явлениями. Существенные в данном аспекте факторы используют далее в регрессионном анализе.
в) Обнаружение неизвестных причинных связей.

Формы проявления взаимосвязей весьма разнообразны. В качестве самых общих их видов выделяют функциональную (полную) и корреляционную (неполную) связи .
Корреляционная связь проявляется в среднем, для массовых наблюдений, когда заданным значениям зависимой переменной соответствует некоторый ряд вероятностных значений независимой переменной. Связь называется корреляционной , если каждому значению факторного признака соответствует вполне определенное неслучайное значение результативного признака.
Наглядным изображением корреляционной таблицы служит корреляционное поле. Оно представляет собой график, где на оси абсцисс откладываются значения X, по оси ординат – Y, а точками показываются сочетания X и Y. По расположению точек можно судить о наличии связи.
Показатели тесноты связи дают возможность охарактеризовать зависимость вариации результативного признака от вариации признака-фактора.
Более совершенным показателем степени тесноты корреляционной связи является линейный коэффициент корреляции . При расчете этого показателя учитываются не только отклонения индивидуальных значений признака от средней, но и сама величина этих отклонений.

Ключевыми вопросами данной темы являются уравнения регрессионной связи между результативным признаком и объясняющей переменной, метод наименьших квадратов для оценки параметров регрессионной модели, анализ качества полученного уравнения регрессии, построение доверительных интервалов прогноза значений результативного признака по уравнению регрессии.

Пример 2

Система нормальных уравнений.
a n + b∑x = ∑y
a∑x + b∑x 2 = ∑y x
Для наших данных система уравнений имеет вид
30a + 5763 b = 21460
5763 a + 1200261 b = 3800360
Из первого уравнения выражаем а и подставим во второе уравнение:
Получаем b = -3.46, a = 1379.33
Уравнение регрессии:
y = -3.46 x + 1379.33

2. Расчет параметров уравнения регрессии.
Выборочные средние.



Выборочные дисперсии:


Среднеквадратическое отклонение


1.1. Коэффициент корреляции
Ковариация .

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < r xy < 0.3: слабая;
0.3 < r xy < 0.5: умеренная;
0.5 < r xy < 0.7: заметная;
0.7 < r xy < 0.9: высокая;
0.9 < r xy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X высокая и обратная.
Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:

1.2. Уравнение регрессии (оценка уравнения регрессии).

Линейное уравнение регрессии имеет вид y = -3.46 x + 1379.33

Коэффициент b = -3.46 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y понижается в среднем на -3.46.
Коэффициент a = 1379.33 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь обратная.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета - коэффициенты.
Средний коэффициент эластичности E показывает, на сколько процентов в среднем по совокупности изменится результат у от своей средней величины при изменении фактора x на 1% от своего среднего значения.
Коэффициент эластичности находится по формуле:


Коэффициент эластичности меньше 1. Следовательно, при изменении Х на 1%, Y изменится менее чем на 1%. Другими словами - влияние Х на Y не существенно.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:

Т.е. увеличение x на величину среднеквадратического отклонения S x приведет к уменьшению среднего значения Y на 0.74 среднеквадратичного отклонения S y .
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации. Средняя ошибка аппроксимации - среднее отклонение расчетных значений от фактических:


Поскольку ошибка меньше 15%, то данное уравнение можно использовать в качестве регрессии.
Дисперсионный анализ.
Задача дисперсионного анализа состоит в анализе дисперсии зависимой переменной:
∑(y i - y cp) 2 = ∑(y(x) - y cp) 2 + ∑(y - y(x)) 2
где
∑(y i - y cp) 2 - общая сумма квадратов отклонений;
∑(y(x) - y cp) 2 - сумма квадратов отклонений, обусловленная регрессией («объясненная» или «факторная»);
∑(y - y(x)) 2 - остаточная сумма квадратов отклонений.
Теоретическое корреляционное отношение для линейной связи равно коэффициенту корреляции r xy .
Для любой формы зависимости теснота связи определяется с помощью множественного коэффициента корреляции :

Данный коэффициент является универсальным, так как отражает тесноту связи и точность модели, а также может использоваться при любой форме связи переменных. При построении однофакторной корреляционной модели коэффициент множественной корреляции равен коэффициенту парной корреляции r xy .
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = -0.74 2 = 0.5413
т.е. в 54.13 % случаев изменения х приводят к изменению y. Другими словами - точность подбора уравнения регрессии - средняя. Остальные 45.87 % изменения Y объясняются факторами, не учтенными в модели.

Список литературы

1. Эконометрика: Учебник / Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001, с. 34..89.
2. Магнус Я.Р., Катышев П.К., Пересецкий А.А. Эконометрика. Начальный курс. Учебное пособие. – 2-е изд., испр. – М.: Дело, 1998, с. 17..42.
3. Практикум по эконометрике: Учеб. пособие / И.И. Елисеева, С.В. Курышева, Н.М. Гордеенко и др.; Под ред. И.И. Елисеевой. – М.: Финансы и статистика, 2001, с. 5..48.

Коэффициенты корреляции

До сих пор мы выясняли лишь сам факт существования статистической зависимости между двумя признаками. Далее мы попробуем выяснить, какие заключения можно сделать о силе или слабости этой зависимости, а также о ее виде и направленности. Критерии количественной оценки зависимости между переменными называются коэффициентами корреляции или мерами связанности. Две переменные коррелируют между собой положительно, если между ними существует прямое, однонаправленное соотношение. При однонаправленном соотношении малые значения одной переменной соответствуют малым значениям другой переменной, большие значения - большим. Две переменные коррелируют между собой отрицательно, если между ними существует обратное, разнонаправленное соотношение. При разнонаправленном соотношении малые значения одной переменной соответствуют большим значениям другой переменной и наоборот. Значения коэффициентов корреляции всегда лежат в диапазоне от -1 до +1.

В качестве коэффициента корреляции между переменными, принадлежащими порядковой шкале применяется коэффициент Спирмена , а для переменных, принадлежащих к интервальной шкале - коэффициент корреляции Пирсона (момент произведений). При этом следует учесть, что каждую дихотомическую переменную, то есть переменную, принадлежащую к номинальной шкале и имеющую две категории, можно рассматривать как порядковую .

Для начала мы проверим существует ли корреляция между переменными sex и psyche из файла studium.sav . При этом дихотомическую переменную sex можно считать порядковой. Выполните следующие действия:

Выберите в меню команды Analyze (Анализ) Descriptive Statistics (Дескриптивные статистики) Crosstabs... (Таблицы сопряженности)

Перенесите переменную sex в список строк, а переменную psyche - в список столбцов.

Щелкните на кнопке Statistics ... (Статистика). В диалоге Crosstabs: Statistics установите флажок Correlations (Корреляции). Подтвердите выбор кнопкой Continue.

В диалоге Crosstabs откажитесь от вывода таблиц, установив флажок Supress tables (Подавлять таблицы). Щелкните на кнопке ОК.

Будут вычислены коэффициенты корреляции Спирмена и Пирсона, а также проведена проверка их значимости:

Symmetric Measures (Симметричные меры)

		Value (Значение)	Asympt. Std. Error (а) (Асимптотическая стандартная ошибка)	Approx. Т (b) (Приблиз. Т)	Approx. Sig. (Приблизительная значимость)
Interval by Interval (Интервальный - интервальный)	Pearson"s R (R Пирсона)	,441	,081	5,006	,000 (с)
Ordinal by Ordinal (Порядковый - Порядковый)	Spearman Correlation (Корреляция по Спирмену)	,439	,083	4,987	,000 (с)
N of Valid Cases (Кол-во допустимых случаев)		106

Так как здесь нет переменных с интервальной шкалой, мы рассмотрим коэффициент корреляции Спирмена. Он составляет 0,439 и является максимально значимым (р<0,001).

Для словесного описания величин коэффициента корреляции применяется следующая таблица:

Исходя из вышеприведенной таблицы, можно сделать следующие заключения: Между переменными sex и psyche существует слабая корреляция (заключение о силе зависимости), переменные коррелируют положительно (заключение о направлении зависимости).

В переменной psyche меньшие значения соответствуют отрицательному психическому состоянию, а большие - положительному. В переменной sex, в свою очередь, значение "1" соответствует женскому полу, а "2" - мужскому.

Следовательно, однонаправленность соотношения можно интерпретировать следующим образом: студентки оценивают свое психическое состояние более негативно, чем ".х коллеги-мужчины или, что вероятнее всего, в большей степени склонны согласиться на такую оценку при проведении анкетирования. Строя подобные интерпретации, нужно учитывать, что корреляция между двумя признаками не обязательно равнозначна их Функциональной или причинной зависимости. Подробнее об этом см. в разделе 15.3.

Теперь проверим корреляцию между переменными alter и semester. Применим методику, описанную выше. Мы получим следующие коэффициенты:

Symmetric Measures

			Asympt. Std. Error (a)
Interval by Interval
Ordinal by Ordinal	Spearman Correlation
N of Valid Cases

a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).

э. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).

с. Based on normal approximation (На основе нормальной аппроксимации).

Так как переменные alter и semester являются метрическими, мы рассмотрим коэффициент Пирсона (момент произведений). Он составляет 0,807. Между переменными alter и semester существует сильная корреляция. Переменные коррелируют положительно. Следовательно, старшие по возрасту студенты учатся на старших курсах, что, собственно, не является неожиданным выводом.

Проверим на корреляцию переменные sozial (оценку социального положения) и psyche. Мы получим следующие коэффициенты:

Symmetric Measures

			Asympt. Std. Error (a)
Interval by Interval
Ordinal by Ordinal	Spearman Correlation
N of Valid Cases

a. Not assuming the null hypothesis (Нулевая гипотеза не принимается).

b. Using the asymptotic standard error assuming the null hypothesis (Используется асимптотическая стандартная ошибка с принятием нулевой гипотезы).

с. Based on normal approximation (На основе нормальной аппроксимации).

В этом случае мы рассмотрим коэффициент корреляции Спирмена; он составляет -0,703. Между переменными sozial и psyche существует средняя или сильная корреляция (граничное значение 0,7). Переменные коррелируют отрицательно, то есть чем больше значения первой переменной, тем меньше значения второй и наоборот. Так как малые значения переменной sozial характеризуют позитивное состояние (1 = очень хорошее, 2 = хорошее), а большие значения psyche - отрицательное состояние (1 = крайне неустойчивое, 2 = неустойчивое), следовательно, психологические затруднения во многом обусловлены социальными проблемами.

Регрессионный анализ позволяет оценить, как одна переменная зависит от другой и каков разброс значений зависимой переменной вокруг прямой, определяющей зависимость. Эти оценки и соответствующие доверительные интервалы позволяют предсказать значение зависимой переменной и определить точность этого предсказания.

Результаты регрессионного анализа можно представить только в достаточно сложной цифровой или графической форме. Однако нас часто интересует не предсказание значения одной переменной по значению другой, а просто характеристика тесноты (силы) связи между ними, при этом выраженная одним числом.

Эта характеристика называется коэффициентом корреляции, обычно ее обозначают буквой г. Коэффициент корреляции мо-

жет принимать значения от -1 до +1. Знак коэффициента корреляции показывает направление связи (прямая или обратная), а абсолютная величина - тесноту связи. Коэффициент, равный -1, определяет столь же жесткую связь, что и равный 1. В отсутствие связи коэффициент корреляции равен нулю.

На рис. 8.10 приведены примеры зависимостей и соответствующие им значения г. Мы рассмотрим два коэффициента корреляции.

Коэффициент корреляции Пирсона предназначен для описания линейной связи количественных признаков; как и регресси
онный анализ, он требует нормальности распределения. Когда говорят просто о «коэффициенте корреляции», почти всегда имеют в виду коэффициент корреляции Пирсона, именно так мы и будем поступать.

Коэффициент ранговой корреляции Спирмена можно использовать, когда связь нелинейна-и не только для количественных, но и для порядковых признаков. Это непараметрический метод, он не требует какого-либо определенного типа распределения.

О количественных, качественных и порядковых признаках мы уже говорили в гл. 5. Количественные признаки - это обычные числовые данные, такие, как рост, вес, температура. Значения количественного признака можно сравнить между собой и сказать, какое из них больше, на сколько и во сколько раз. Например, если один марсианин весит 15 г, а другой 10, то первый тяжелее второго и в полтора раза и на 5 г. Значения порядкового признака тоже можно сравнить, сказав, какое из них больше, но нельзя сказать, ни на сколько, ни во сколько раз. В медицине порядковые признаки встречаются довольно часто. Например, результаты исследования влагалищного мазка по Папаниколау оценивают по такой шкале: 1) норма, 2) легкая дисплазия, 3) умеренная дисплазия, 4) тяжелая дисплазия, 5) рак in situ. И количественные, и порядковые признаки можно расположить по порядку - на этом общем свойстве основана большая группа непараметрических критериев, к которым относится и коэффициент ранговой корреляции Спирмена. С другими непараметрическими критериями мы познакомимся в гл. 10.

Коэффициент корреляции Пирсона

И все же, почему для описания тесноты связи нельзя воспользоваться регрессионным анализом? В качестве меры тесноты связи можно было бы использовать остаточное стандартное отклонение. Однако если поменять местами зависимую и независимую переменные, то остаточное стандартное отклонение, как и другие показатели регрессионного анализа, будет иным.

Взглянем на рис. 8.11. По известной нам выборке из 10 марсиан построены две линии регрессии. В одном случае вес - зависимая переменная, во втором - независимая. Линии регрессии заметно разли-

20

Если поменять местами х и у, уравнение регрессии получится другим, а коэф- ■ корреляции останется прежним.

чаются. Получается, что связь роста с весом одна, а веса с ростом - другая. Асимметричность регрессионного анализа - вот что мешает непосредственно использовать его для характеристики силы связи. Коэффициент корреляции, хотя его идея вытекает из регрессионного анализа, свободен от этого недостатка. Приводим формулу.

r Y(X - X)(Y - Y)

&((- X) S(y - Y)2"

где X и Y - средние значения переменных X и Y. Выражение для r «симметрично» -поменяв местами Xи Y, мы получим ту же величину. Коэффициент корреляции принимает значения от -1 до +1. Чем теснее связь, тем больше абсолютная величина коэффициента корреляции. Знак показывает направление связи. При r > 0 говорят о прямой корреляции (с увеличением одной переменной другая также возрастает), при r Возьмем пример с 10 марсианами, который мы уже рассматривали с точки зрения регрессионного анализа. Вычислим коэффициент корреляции. Исходные данные и промежуточные результаты вычислений приведены в табл. 8.3. Объем выборки n = 10, средний рост

X = £ X/n = 369/10 = 36,9 и вес Y = £ Y/n = 103,8/10 = 10,38.

Находим Щ- X)(Y- Y) = 99,9, Щ- X)2 = 224,8, £(Y - Y)2 = 51,9.

Подставим полученные значения в формулу для коэффициента корреляции:

224,8 х 51,9 ’ "

Величина r близка к 1, что говорит о тесной связи роста и веса. Чтобы лучше представить себе, какой коэффициент корреляции следует считать большим, а какой незначительным, взгляни-

Таблица 8.3. Вычисление коэффициента корреляции X Y X -X Y-Y (X -X)(Y-Y) (X -X)2 (Y-Y)2 31 7,8 -5,9 -2,6 15,3 34,8 6,8 32 8,3 -4,9 -2,1 10,3 24,0 4,4 33 7,6 -3,9 -2,8 10,9 15,2 7,8 34 9,1 -2,9 -1,3 3,8 8,4 1,7 35 9,6 -1,9 -0,8 1,5 3,6 0,6 35 9,8 -1,9 -0,6 1,1 3,6 0,4 40 11,8 3,1 1,4 4,3 9,6 2,0 41 12,1 4,1 1,7 7,0 16,8 2,9 42 14,7 5,1 4,3 22,0 26,0 18,5 46 13,0 9,1 2,6 23,7 82,8 6,8 369 103,8 0,0 0,2 99,9 224,8 51,9

те на табл. 8.4 - в ней приведены коэффициенты корреляции для примеров, которые мы разбирали ранее.

Связь регрессии и корреляции

Все примеры коэффициентов корреляции (табл. 8.4) мы первоначально использовали для построения линий регрессии. Действительно, между коэффициентом корреляции и параметрами регрессионного анализа существует тесная связь, которую мы сейчас продемонстрируем. Разные способы представления коэффициента корреляции, которые мы при этом получим, позволят лучше понять смысл этого показателя.

Вспомним, что уравнение регрессии строится так, чтобы минимизировать сумму квадратов отклонений от линии регрессии.

Обозначим эту минимальную сумму квадратов S (эту величину называют остаточной суммой квадратов). Сумму квадратов отклонений значений зависимой переменной Y от ее среднего Y обозначим S^. Тогда:

Величина г2 называется коэффициентом детерминации - это просто квадрат коэффициента корреляции. Коэффициент детерминации показывает силу связи, но не ее направленность.

Из приведенной формулы видно, что если значения зависимой переменной лежат на прямой регрессии, то S = 0, и тем самым r = +1 или r = -1, то есть существует линейная связь зависимой и независимой переменной. По любому значению независимой переменной можно совершенно точно предсказать значение зависимой переменной. Напротив, если переменные вообще не связаны между собой, то Soci = SofSisi Тогда r = 0.

Видно также, что коэффициент детерминации равен той доле общей дисперсии S^, которая обусловлена или, как говорят, объясняется линейной регрессией.

Остаточная сумма квадратов S связана с остаточной дисперсией s2y\x соотношением Socj = (п - 2) s^, а общая сумма квадратов S^ с дисперсией s2 соотношением S^ = (п - 1)s2 . В таком случае

r2 = 1 _ n _ 2 sy\x п _1 sy

Эта формула позволяет судить о зависимости коэффициента корреляции от доли остаточной дисперсии в полной дисперсии

six/s2y Чем эта доля меньше, тем больше (по абсолютной величине) коэффициент корреляции, и наоборот.

Мы убедились, что коэффициент корреляции отражает тесноту линейной связи переменных. Однако если речь идет о предсказании значения одной переменной по значению другой, на
коэффициент корреляции не следует слишком полагаться. Например, данным на рис. 8.7 соответствует весьма высокий коэффициент корреляции (г = 0,92), однако ширина доверительной области значений показывает, что неопределенность предсказания довольно значительна. Поэтому даже при большом коэффициенте корреляции обязательно вычислите доверительную область значений.

И под конец приведем соотношение коэффициента корреляции и коэффициента наклона прямой регрессии b:

где b - коэффициент наклона прямой регрессии, sx и sY - стандартные отклонения переменных.

Если не брать во внимание случай sx = 0, то коэффициент корреляции равен нулю тогда и только тогда, когда b = 0. Этим фактом мы сейчас и воспользуемся для оценки статистической значимости корреляции.

Статистическая значимость корреляции

Поскольку из b = 0 следует г = 0, гипотеза об отсутствии корреляции равнозначна гипотезе о нулевом наклоне прямой регрессии. Поэтому для оценки статистической значимости корреляции можно воспользоваться уже известной нам формулой для оценки статистической значимости отличия b от нуля:

Здесь число степеней свободы v = n - 2. Однако если коэффициент корреляции уже вычислен, удобнее воспользоваться формулой:

Число степеней свободы здесь также v = п - 2.

При внешнем несходстве двух формул для t, они тождественны. Действительно, из того, что

r 2 _ 1 - n_ 2 Sy]x_

Подставив значение sy^x в формулу для стандартной ошибки

Животный жир и рак молочной железы

В опытах на лабораторных животных показано, что высокое содержание животного жира в рационе повышает риск рака молочной железы. Наблюдается ли эта зависимость у людей? К. Кэррол собрал данные о потреблении животных жиров и смертности от рака молочной железы по 39 странам. Результат представлен на рис. 8.12А. Коэффициент корреляции между потреблением животных жиров и смертностью от рака молочной железы оказался равен 0,90. Оценим статистическую значимость корреляции.

0,90 1 - 0,902 39 - 2

Критическое значение t при числе степеней свободы v = 39 - 2 = 37 равно 3,574, то Єсть меньше полученного нами. Таким образом, при уровне значимости 0,001 можно утверждать, что существует корреляция между потреблением животных жиров и смертностью от рака молочной железы.

Теперь проверим, связана ли смертность с потреблением растительных жиров? Соответствующие данные приведены на рис. 8.12Б. Коэффициент корреляции равен 0,15. Тогда

1 - 0,152 39 - 2

Даже при уровне значимости 0,10 вычисленное значение t меньше критического. Корреляция статистически не значима.

Коэффициент корреляции (или линейный коэффициент корреляции) обозначается как «r» (в редких случаях как «ρ») и характеризует линейную корреляцию (то есть взаимосвязь, которая задается некоторым значением и направлением) двух или более переменных. Значение коэффициента лежит между -1 и +1, то есть корреляция бывает как положительной, так и отрицательной. Если коэффициент корреляции равен -1, имеет место идеальная отрицательная корреляция; если коэффициент корреляции равен +1, имеет место идеальная положительная корреляция. В остальных случаях между двумя переменными наблюдается положительная корреляция, отрицательная корреляция или отсутствие корреляции. Коэффициент корреляции можно вычислить вручную, с помощью бесплатных онлайн-калькуляторов или с помощью хорошего графического калькулятора.

Шаги

Вычисление коэффициента корреляции вручную

Соберите данные. Перед тем как приступить к вычислению коэффициента корреляции, изучите данные пары чисел. Лучше записать их в таблицу, которую можно расположить вертикально или горизонтально. Каждую строку или столбец обозначьте как «х» и «у».

• Например, даны четыре пары значений (чисел) переменных «х» и «у». Можно создать следующую таблицу:
  • x || y
  • 1 || 1
  • 2 || 3
  • 4 || 5
  • 5 || 7

1. Вычислите среднее арифметическое «х». Для этого сложите все значения «х», а затем полученный результат разделите на количество значений.

   Найдите среднее арифметическое «у». Для этого выполните аналогичные действия, то есть сложите все значения «у», а затем сумму разделите на количество значений.

   Вычислите стандартное отклонение «х». Вычислив средние значения «х» и «у», найдите стандартные отклонения этих переменных. Стандартное отклонение вычисляется по следующей формуле:

   Вычислите стандартное отклонение «у». Выполните действия, которые описаны в предыдущем шаге. Воспользуйтесь той же формулой, но подставьте в нее значения «у».

   Запишите основную формулу для вычисления коэффициента корреляции. В эту формулу входят средние значения, стандартные отклонения и количество (n) пар чисел обеих переменных. Коэффициент корреляции обозначается как «r» (в редких случаях как «ρ»). В этой статье используется формула для вычисления коэффициента корреляции Пирсона.

   Вы вычислили средние значения и стандартные отклонения обеих переменных, поэтому можно воспользоваться формулой для вычисления коэффициента корреляции. Напомним, что «n» – это количество пар значений обеих переменных. Значение других величин были вычислены ранее.

   • В нашем примере вычисления запишутся так:
   • ρ = (1 n − 1) Σ (x − μ x σ x) ∗ (y − μ y σ y) {\displaystyle \rho =\left({\frac {1}{n-1}}\right)\Sigma \left({\frac {x-\mu _{x}}{\sigma _{x}}}\right)*\left({\frac {y-\mu _{y}}{\sigma _{y}}}\right)}
   • ρ = (1 3) ∗ {\displaystyle \rho =\left({\frac {1}{3}}\right)*} [ (1 − 3 1 , 83) ∗ (1 − 4 2 , 58) + (2 − 3 1 , 83) ∗ (3 − 4 2 , 58) {\displaystyle \left({\frac {1-3}{1,83}}\right)*\left({\frac {1-4}{2,58}}\right)+\left({\frac {2-3}{1,83}}\right)*\left({\frac {3-4}{2,58}}\right)}
     + (4 − 3 1 , 83) ∗ (5 − 4 2 , 58) + (5 − 3 1 , 83) ∗ (7 − 4 2 , 58) {\displaystyle +\left({\frac {4-3}{1,83}}\right)*\left({\frac {5-4}{2,58}}\right)+\left({\frac {5-3}{1,83}}\right)*\left({\frac {7-4}{2,58}}\right)} ]
   • ρ = (1 3) ∗ (6 + 1 + 1 + 6 4 , 721) {\displaystyle \rho =\left({\frac {1}{3}}\right)*\left({\frac {6+1+1+6}{4,721}}\right)}
   • ρ = (1 3) ∗ 2 , 965 {\displaystyle \rho =\left({\frac {1}{3}}\right)*2,965}
   • ρ = (2 , 965 3) {\displaystyle \rho =\left({\frac {2,965}{3}}\right)}
   • ρ = 0 , 988 {\displaystyle \rho =0,988}

2. Проанализируйте полученный результат. В нашем примере коэффициент корреляции равен 0,988. Это значение некоторым образом характеризует данный набор пар чисел. Обратите внимание на знак и величину значения.

   • Так как значение коэффициента корреляции положительно, между переменными «х» и «у» имеет место положительная корреляция. То есть при увеличении значения «х», значение «у» тоже увеличивается.
   • Так как значение коэффициента корреляции очень близко к +1, значения переменных «х» и «у» сильно взаимосвязаны. Если нанести точки на координатную плоскость, они расположатся близко к некоторой прямой.

   Использование онлайн-калькуляторов для вычисления коэффициента корреляции

   1. В интернете найдите калькулятор для вычисления коэффициента корреляции. Этот коэффициент довольно часто вычисляется в статистике. Если пар чисел много, вычислить коэффициент корреляции вручную практически невозможно. Поэтому существуют онлайн-калькуляторы для вычисления коэффициента корреляции. В поисковике введите «коэффициент корреляции калькулятор» (без кавычек).

      Введите данные. Ознакомьтесь с инструкциями на сайте, чтобы правильно ввести данные (пары чисел). Крайне важно вводить соответствующие пары чисел; в противном случае вы получите неверный результат. Помните, что на разных веб-сайтах различные форматы ввода данных.

      • Например, на сайте http://ncalculators.com/statistics/correlation-coefficient-calculator.htm значения переменных «х» и «у» вводятся в двух горизонтальных строках. Значения разделяются запятыми. То есть в нашем примере значения «х» вводятся так: 1,2,4,5, а значения «у» так: 1,3,5,7.
      • На другом сайте, http://www.alcula.com/calculators/statistics/correlation-coefficient/ , данные вводятся по вертикали; в этом случае не перепутайте соответствующие пары чисел.

   2. Вычислите коэффициент корреляции. Введя данные, просто нажмите на кнопку «Calculate», «Вычислить» или аналогичную, чтобы получить результат.

   Использование графического калькулятора

   1. Введите данные. Возьмите графический калькулятор, перейдите в режим статистических вычислений и выберите команду «Edit» (Редактировать).

      • На разных калькуляторах нужно нажимать различные клавиши. В этой статье рассматривается калькулятор Texas Instruments TI-86.
      • Чтобы перейти в режим статистических вычислений, нажмите – Stat (над клавишей «+»). Затем нажмите F2 – Edit (Редактировать).

   2. Удалите предыдущие сохраненные данные. В большинстве калькуляторов введенные статистические данные хранятся до тех пор, пока вы не сотрете их. Чтобы не спутать старые данные с новыми, сначала удалите любую сохраненную информацию.

      • С помощью клавиш со стрелками переместите курсор и выделите заголовок «xStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец xStat.
      • С помощью клавиш со стрелками выделите заголовок «yStat». Затем нажмите Clear (Очистить) и Enter (Ввести), чтобы удалить все значения, введенные в столбец уStat.

   3. Введите исходные данные. С помощью клавиш со стрелками переместите курсор в первую ячейку под заголовком «xStat». Введите первое значение и нажмите Enter. В нижней части экрана отобразится «xStat (1) = __», где вместо пробела будет стоять введенное значение. После того как вы нажмете Enter, введенное значение появится в таблице, а курсор переместится на следующую строку; при этом в нижней части экрана отобразится «xStat (2) = __».

      • Введите все значения переменной «х».
      • Введя все значения переменной «х», с помощью клавиш со стрелками перейдите в столбец yStat и введите значения переменной «у».
      • После ввода всех пар чисел нажмите Exit (Выйти), чтобы очистить экран и выйти из режима статистических вычислений.

» Статистика

Статистика и обработка данных в психологии
(продолжение)

Корреляционный анализ

При изучении корреляций стараются установить, существует ли какая-то связь между двумя показателями в одной выборке (например, между ростом и весом детей или между уровнем IQ и школьной успеваемостью) либо между двумя различными выборками (например, при сравнении пар близнецов), и если эта связь существует, то сопровождается ли увеличение одного показателя возрастанием (положительная корреляция) или уменьшением (отрицательная корреляция) другого.

Иными словами, корреляционный анализ помогает установить, можно ли предсказывать возможные значения одного показателя, зная величину другого.

До сих пор при анализе результатов нашего опыта по изучению действия марихуаны мы сознательно игнорировали такой показатель, как время реакции. Между тем было бы интересно проверить, существует ли связь между эффективностью реакций и их быстротой. Это позволило бы, например, утверждать, что чем человек медлительнее, тем точнее и эффективнее будут его действия и наоборот.

С этой целью можно использовать два разных способа: параметрический метод расчета коэффициента Браве-Пирсона (r) и вычисление коэффициента корреляции рангов Спирмена (r s), который применяется к порядковым данным, т.е. является непараметрическим. Однако разберемся сначала в том, что такое коэффициент корреляции.

Коэффициент корреляции

Коэффициент корреляции - это величина, которая может варьировать в пределах от +1 до -1. В случае полной положительной корреляции этот коэффициент равен плюс 1, а при полной отрицательной - минус 1. На графике этому соответствует прямая линия, проходящая через точки пересечения значений каждой пары данных:

В случае же если эти точки не выстраиваются по прямой линии, а образуют «облако», коэффициент корреляции по абсолютной величине становится меньше единицы и по мере округления этого облака приближается к нулю:

В случае если коэффициент корреляции равен 0, обе переменные полностью независимы друг от друга.

В гуманитарных науках корреляция считается сильной, если ее коэффициент выше 0,60; если же он превышает 0,90, то корреляция считается очень сильной. Однако для того, чтобы можно было делать выводы о связях между переменными, большое значение имеет объем выборки: чем выборка больше, тем достовернее величина полученного коэффициента корреляции. Существуют таблицы с критическими значениями коэффициента корреляции Браве-Пирсона и Спирмена для разного числа степеней свободы (оно равно числу пар за вычетом 2, т. е. n- 2). Лишь в том случае, если коэффициенты корреляции больше этих критических значений, они могут считаться достоверными. Так, для того чтобы коэффициент корреляции 0,70 был достоверным, в анализ должно быть взято не меньше 8 пар данных (h =n -2=6) при вычислении r (см. табл. 4 в Приложении) и 7 пар данных (h =n-2= 5) при вычислении r s (табл. 5 в Приложении).

Хотелось бы еще раз подчеркнуть, что сущность этих двух коэффициентов несколько различна. Отрицательный коэффициент r указывает на то, что эффективность чаще всего тем выше, чем время реакции меньше, тогда как при вычислении коэффициента r s требовалось проверить, всегда ли более быстрые испытуемые реагируют более точно, а более медленные - менее точно.

Коэффициент корреляции Браве-Пирсона (r) - этопараметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений. При этом используют формулу (у разных авторов она может выглядеть по-разному)

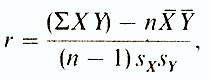
где ΣXY - сумма произведений данных из каждой пары;
n-число пар;
X - средняя для данных переменной X;
Y - средняя для данных переменной Y
S x - стандартное отклонение для распределения х;
S y - стандартное отклонение для распределения у

Коэффициент корреляции рангов Спирмена (r s ) - это непараметрический показатель, с помощью которого пытаются выявить связь между рангами соответственных величин в двух рядах измерений.

Этот коэффициент рассчитывать проще, однако результаты получаются менее точными, чем при использовании r. Это связано с тем, что при вычислении коэффициента Спирмена используют порядок следования данных, а не их количественные характеристики и интервалы между классами.

Дело в том, что при использовании коэффициента корреляции рангов Спирмена (r s) проверяют только, будет ли ранжирование данных для какой-либо выборки таким же, как и в ряду других данных для этой выборки, попарно связанных с первыми (например, будут ли одинаково «ранжироваться» студенты при прохождении ими как психологии, так и математики, или даже при двух разных преподавателях психологии?). Если коэффициент близок к +1, то это означает, что оба ряда практически совпадают, а если этот коэффициент близок к -1, можно говорить о полной обратной зависимости.

Коэффициент r s вычисляют по формуле

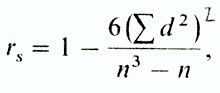
где d - разность между рангами сопряженных значений признаков (независимо от ее знака), а - число пар.

Обычно этот непараметрический тест используется в тех случаях, когда нужно сделать какие-то выводы не столько об интервалах между данными, сколько об их рангах, а также тогда, когда кривые распределения слишком асимметричны и не позволяют использовать такие параметрические критерии, как коэффициент r (в этих случаях бывает необходимо превратить количественные данные в порядковые).

Резюме

Итак, мы рассмотрели различные параметрические и непараметрические статистические методы, используемые в психологии. Наш обзор был весьма поверхностным, и главная задача его заключалась в том, чтобы читатель понял, что статистика не так страшна, как кажется, и требует в основном здравого смысла. Напоминаем, что данные «опыта», с которыми мы здесь имели дело, - вымышленные и не могут служить основанием для каких-либо выводов. Впрочем, подобный эксперимент стоило бы действительно провести. Поскольку для этого опыта была выбрана сугубо классическая методика, такой же статистический анализ можно было бы использовать во множестве различных экспериментов. В любом случае нам кажется, что мы наметили какие-то главные направления, которые могут оказаться полезны тем, кто не знает, с чего начать статистический анализ полученных результатов.

Литература

1. Годфруа Ж. Что такое психология. - М., 1992.
2. Chatillon G., 1977. Statistique en Sciences humaines, Trois-Rivieres, Ed. SMG.
3. Gilbert N.. 1978. Statistiques, Montreal, Ed. HRW.
4. Moroney M.J., 1970. Comprendre la statistique, Verviers, Gerard et Cie.
5. Siegel S., 1956. Non-parametric Statistic, New York, MacGraw-Hill Book Co.

Приложение Таблицы

Примечания. 1) Для больших выборок или уровня значимости меньше 0,05 следует обратиться к таблицам в пособиях по статистике.

2) Таблицы значений других непараметрических критериев можно найти в специальных руководствах (см. библиографию).

Таблица 1. Значения критерия t Стьюдента
h	0,05
1	6,31
2	2,92
3	2,35
4	2,13
5	2,02
6	1,94
7	1,90
8	1,86
9	1,83
10	1,81
11	1,80
12	1,78
13	1,77
14	1,76
15	1,75
16	1,75
17	1,74
18	1,73
19	1,73
20	1,73
21	1,72
22	1,72
23	1,71
24	1,71
25	1,71
26	1,71
27	1,70
28	1,70
29	1,70
30	1,70
40	1,68
¥	1,65

Таблица 2. Значения критерия χ 2
h	0,05
1	3,84
2	5,99
3	7,81
4	9,49
5	11,1
6	12,6
7	14,1
8	15,5
9	16,9
10	18,3
Таблица 3. Достоверные значения Z
р	Z
0,05	1,64
0,01	2,33

Таблица 4. Достоверные (критические) значения r
h =(N-2)		р= 0,05 (5%)
3		0,88
4		0,81
5		0,75
6		0,71
7		0,67
8		0,63
9		0,60
10		0,58
11		0.55
12		0,53
13		0,51
14		0,50
15		0,48
16		0,47
17		0,46
18		0,44
19		0,43
20		0,42

Таблица 5. Достоверные (критические) значения r s
h =(N-2)	р = 0,05
2	1,000
3	0,900
4	0,829
5	0,714
6	0,643
7	0,600
8	0,564
10	0,506
12	0,456
14	0,425
16	0,399
18	0,377
20	0,359
22	0,343
24	0,329
26	0,317
28	0,306